363318
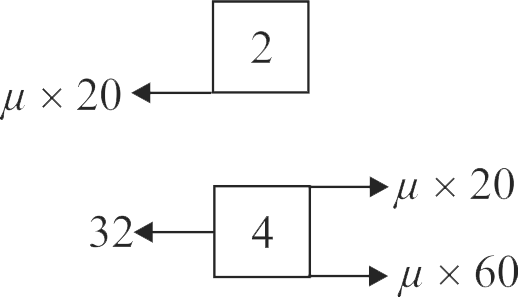
Figure (a) shows a block \({B}\) of mass \(4\,kg\) kept on a rough ground, with a block \({A}\) of mass \(2\,kg\) kept upon it. When a horizontal force \({F=32 {~N}}\) is applied to block \({B}\), the relative acceleration of \({B}\) \(w.r.t.\) \({A}\) is shown in Fig. (b), plotted against time. If the roughness coefficient \({(\mu)}\) between the surfaces of \({A}\) and \({B}\) and that between \({B}\) and ground be the same. The value of \({\mu\left(g=10 {~m} / {s}^{2}\right)}\) is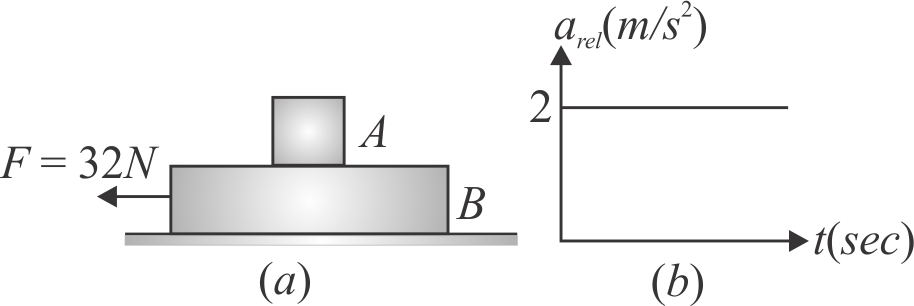
363319
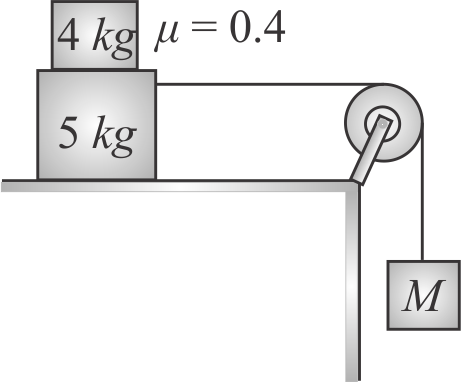
Two masses \({m_1} = 10\;kg\) and \({m_2} = 20\;kg,\) connected by an inextensible string over a frictionless pulley, are moving as shown in the figure.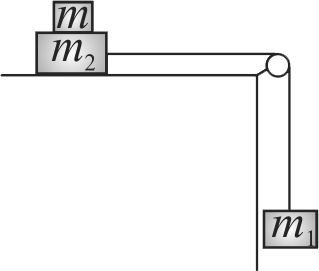
The coefficient of friction of horizontal surface is \(0.30.\) Then what is the minimum weight \(m\) that should be put on top of \({m_2}\) to stop the motion
363320
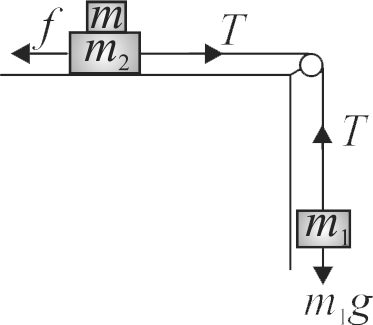
A \(40\,kg\) slab rests on a frictionless floor. A \(10\,kg\) block rests on top of the slab as shown in the figure. The coefficient of static friction between the block and slab is 0.60 and coefficient of kinetic friction is 0.40. The \(10\,kg\) block is acted upon by a horizontal force of \(100\,N\). What is the resulting acceleration of slab (in \({m/{s^2}}\)) (Take \({g=10 {~m} / {s}^{2}}\)) is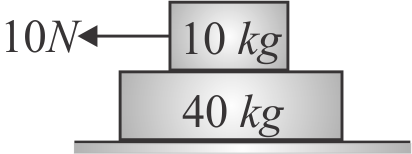
363321
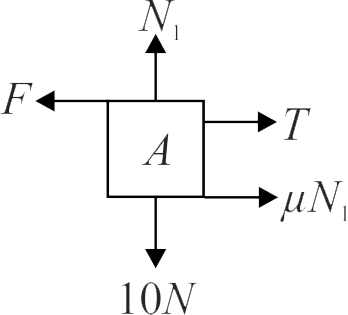
Two blocks \({A(1 {~kg})}\) and \({B(2 {~kg})}\) are connected by a string passing over a smooth pulley as shown in the figure. \({B}\) rests on rough horizontal surface and \({A}\) rests on \({B}\). The coefficient of friction between \({A}\) and \({B}\) is the same as that between \({B}\) and the horizontal surface. The minimum horizontal force \({F}\) required to move \({A}\) to the left is \(25\,N\). What is the coefficient of friction \({\left(g=10 {~m} / {s}^{2}\right)}\) is
363318
Figure (a) shows a block \({B}\) of mass \(4\,kg\) kept on a rough ground, with a block \({A}\) of mass \(2\,kg\) kept upon it. When a horizontal force \({F=32 {~N}}\) is applied to block \({B}\), the relative acceleration of \({B}\) \(w.r.t.\) \({A}\) is shown in Fig. (b), plotted against time. If the roughness coefficient \({(\mu)}\) between the surfaces of \({A}\) and \({B}\) and that between \({B}\) and ground be the same. The value of \({\mu\left(g=10 {~m} / {s}^{2}\right)}\) is
363319
Two masses \({m_1} = 10\;kg\) and \({m_2} = 20\;kg,\) connected by an inextensible string over a frictionless pulley, are moving as shown in the figure.
The coefficient of friction of horizontal surface is \(0.30.\) Then what is the minimum weight \(m\) that should be put on top of \({m_2}\) to stop the motion
363320
A \(40\,kg\) slab rests on a frictionless floor. A \(10\,kg\) block rests on top of the slab as shown in the figure. The coefficient of static friction between the block and slab is 0.60 and coefficient of kinetic friction is 0.40. The \(10\,kg\) block is acted upon by a horizontal force of \(100\,N\). What is the resulting acceleration of slab (in \({m/{s^2}}\)) (Take \({g=10 {~m} / {s}^{2}}\)) is
363321
Two blocks \({A(1 {~kg})}\) and \({B(2 {~kg})}\) are connected by a string passing over a smooth pulley as shown in the figure. \({B}\) rests on rough horizontal surface and \({A}\) rests on \({B}\). The coefficient of friction between \({A}\) and \({B}\) is the same as that between \({B}\) and the horizontal surface. The minimum horizontal force \({F}\) required to move \({A}\) to the left is \(25\,N\). What is the coefficient of friction \({\left(g=10 {~m} / {s}^{2}\right)}\) is
363318
Figure (a) shows a block \({B}\) of mass \(4\,kg\) kept on a rough ground, with a block \({A}\) of mass \(2\,kg\) kept upon it. When a horizontal force \({F=32 {~N}}\) is applied to block \({B}\), the relative acceleration of \({B}\) \(w.r.t.\) \({A}\) is shown in Fig. (b), plotted against time. If the roughness coefficient \({(\mu)}\) between the surfaces of \({A}\) and \({B}\) and that between \({B}\) and ground be the same. The value of \({\mu\left(g=10 {~m} / {s}^{2}\right)}\) is
363319
Two masses \({m_1} = 10\;kg\) and \({m_2} = 20\;kg,\) connected by an inextensible string over a frictionless pulley, are moving as shown in the figure.
The coefficient of friction of horizontal surface is \(0.30.\) Then what is the minimum weight \(m\) that should be put on top of \({m_2}\) to stop the motion
363320
A \(40\,kg\) slab rests on a frictionless floor. A \(10\,kg\) block rests on top of the slab as shown in the figure. The coefficient of static friction between the block and slab is 0.60 and coefficient of kinetic friction is 0.40. The \(10\,kg\) block is acted upon by a horizontal force of \(100\,N\). What is the resulting acceleration of slab (in \({m/{s^2}}\)) (Take \({g=10 {~m} / {s}^{2}}\)) is
363321
Two blocks \({A(1 {~kg})}\) and \({B(2 {~kg})}\) are connected by a string passing over a smooth pulley as shown in the figure. \({B}\) rests on rough horizontal surface and \({A}\) rests on \({B}\). The coefficient of friction between \({A}\) and \({B}\) is the same as that between \({B}\) and the horizontal surface. The minimum horizontal force \({F}\) required to move \({A}\) to the left is \(25\,N\). What is the coefficient of friction \({\left(g=10 {~m} / {s}^{2}\right)}\) is
363318
Figure (a) shows a block \({B}\) of mass \(4\,kg\) kept on a rough ground, with a block \({A}\) of mass \(2\,kg\) kept upon it. When a horizontal force \({F=32 {~N}}\) is applied to block \({B}\), the relative acceleration of \({B}\) \(w.r.t.\) \({A}\) is shown in Fig. (b), plotted against time. If the roughness coefficient \({(\mu)}\) between the surfaces of \({A}\) and \({B}\) and that between \({B}\) and ground be the same. The value of \({\mu\left(g=10 {~m} / {s}^{2}\right)}\) is
363319
Two masses \({m_1} = 10\;kg\) and \({m_2} = 20\;kg,\) connected by an inextensible string over a frictionless pulley, are moving as shown in the figure.
The coefficient of friction of horizontal surface is \(0.30.\) Then what is the minimum weight \(m\) that should be put on top of \({m_2}\) to stop the motion
363320
A \(40\,kg\) slab rests on a frictionless floor. A \(10\,kg\) block rests on top of the slab as shown in the figure. The coefficient of static friction between the block and slab is 0.60 and coefficient of kinetic friction is 0.40. The \(10\,kg\) block is acted upon by a horizontal force of \(100\,N\). What is the resulting acceleration of slab (in \({m/{s^2}}\)) (Take \({g=10 {~m} / {s}^{2}}\)) is
363321
Two blocks \({A(1 {~kg})}\) and \({B(2 {~kg})}\) are connected by a string passing over a smooth pulley as shown in the figure. \({B}\) rests on rough horizontal surface and \({A}\) rests on \({B}\). The coefficient of friction between \({A}\) and \({B}\) is the same as that between \({B}\) and the horizontal surface. The minimum horizontal force \({F}\) required to move \({A}\) to the left is \(25\,N\). What is the coefficient of friction \({\left(g=10 {~m} / {s}^{2}\right)}\) is
363318
Figure (a) shows a block \({B}\) of mass \(4\,kg\) kept on a rough ground, with a block \({A}\) of mass \(2\,kg\) kept upon it. When a horizontal force \({F=32 {~N}}\) is applied to block \({B}\), the relative acceleration of \({B}\) \(w.r.t.\) \({A}\) is shown in Fig. (b), plotted against time. If the roughness coefficient \({(\mu)}\) between the surfaces of \({A}\) and \({B}\) and that between \({B}\) and ground be the same. The value of \({\mu\left(g=10 {~m} / {s}^{2}\right)}\) is
363319
Two masses \({m_1} = 10\;kg\) and \({m_2} = 20\;kg,\) connected by an inextensible string over a frictionless pulley, are moving as shown in the figure.
The coefficient of friction of horizontal surface is \(0.30.\) Then what is the minimum weight \(m\) that should be put on top of \({m_2}\) to stop the motion
363320
A \(40\,kg\) slab rests on a frictionless floor. A \(10\,kg\) block rests on top of the slab as shown in the figure. The coefficient of static friction between the block and slab is 0.60 and coefficient of kinetic friction is 0.40. The \(10\,kg\) block is acted upon by a horizontal force of \(100\,N\). What is the resulting acceleration of slab (in \({m/{s^2}}\)) (Take \({g=10 {~m} / {s}^{2}}\)) is
363321
Two blocks \({A(1 {~kg})}\) and \({B(2 {~kg})}\) are connected by a string passing over a smooth pulley as shown in the figure. \({B}\) rests on rough horizontal surface and \({A}\) rests on \({B}\). The coefficient of friction between \({A}\) and \({B}\) is the same as that between \({B}\) and the horizontal surface. The minimum horizontal force \({F}\) required to move \({A}\) to the left is \(25\,N\). What is the coefficient of friction \({\left(g=10 {~m} / {s}^{2}\right)}\) is