Explanation:
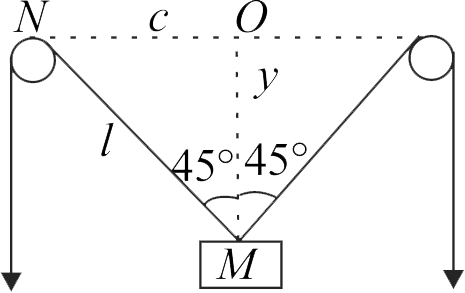
In right angled \(\Delta MNO\), \({l^2} = {c^2} + {y^2}\)
Differentiating w.r.t. time, we get,
\(2l\frac{{dl}}{{dt}} = 0 + 2y\frac{{dy}}{{dt}}\)
\(\therefore \quad \frac{{dy}}{{dt}} = \frac{l}{y}\frac{{dl}}{{dt}}\)
Now, \(\frac{{dy}}{{dt}} = {v_m};\frac{l}{y}\)
\(\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{{\cos 45^\circ }};\frac{{dl}}{{dt}} = 5\)
\(\therefore \quad {v_m} = \frac{5}{{\cos 45^\circ }}\)
\(\therefore \quad {v_m} = 7.05\;m{\rm{/}}s\)