363208
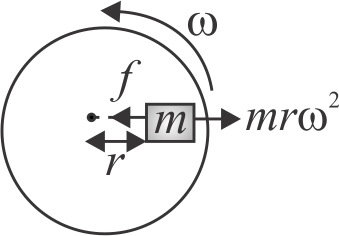
A small ring \(P\) is threaded on a smooth wire bent in the form of a circle of radius \(a\) and center \(O\). The wire is rotating with constant angular speed \(\omega \) about a vertical diameter \(XY\), while the ring remains at rest relative to the wire at a distance \(a\)/2 from \(XY\). Then \({\omega ^2}\) is equal to.png)
363209
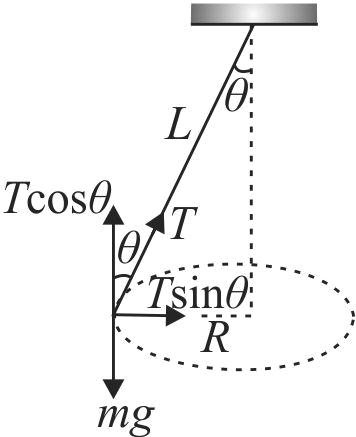
A ball of mass \((m)0.5\;kg\) is attached to the end of a string having length \((L)0.5\;m\). The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is \(324\,N\). The maximum possible value of angular velocity of ball (in radian/s) is
363208
A small ring \(P\) is threaded on a smooth wire bent in the form of a circle of radius \(a\) and center \(O\). The wire is rotating with constant angular speed \(\omega \) about a vertical diameter \(XY\), while the ring remains at rest relative to the wire at a distance \(a\)/2 from \(XY\). Then \({\omega ^2}\) is equal to.png)
363209
A ball of mass \((m)0.5\;kg\) is attached to the end of a string having length \((L)0.5\;m\). The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is \(324\,N\). The maximum possible value of angular velocity of ball (in radian/s) is
363208
A small ring \(P\) is threaded on a smooth wire bent in the form of a circle of radius \(a\) and center \(O\). The wire is rotating with constant angular speed \(\omega \) about a vertical diameter \(XY\), while the ring remains at rest relative to the wire at a distance \(a\)/2 from \(XY\). Then \({\omega ^2}\) is equal to.png)
363209
A ball of mass \((m)0.5\;kg\) is attached to the end of a string having length \((L)0.5\;m\). The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is \(324\,N\). The maximum possible value of angular velocity of ball (in radian/s) is
363208
A small ring \(P\) is threaded on a smooth wire bent in the form of a circle of radius \(a\) and center \(O\). The wire is rotating with constant angular speed \(\omega \) about a vertical diameter \(XY\), while the ring remains at rest relative to the wire at a distance \(a\)/2 from \(XY\). Then \({\omega ^2}\) is equal to.png)
363209
A ball of mass \((m)0.5\;kg\) is attached to the end of a string having length \((L)0.5\;m\). The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is \(324\,N\). The maximum possible value of angular velocity of ball (in radian/s) is