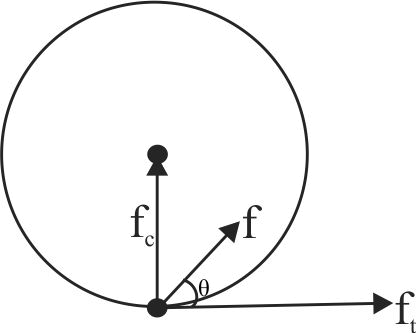
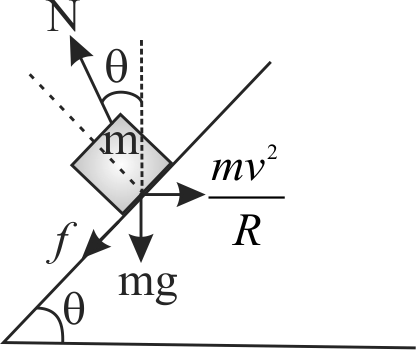
363189 A child starts running from rest along a circular track of radius \(r\) with constant tangential acceleration \(a\). After time \(t\) he feels that slipping of shoes on the ground has started. The coefficient of friction between shoes and the ground is[ \(g\) \(=\) acceleration due to gravity]
363189 A child starts running from rest along a circular track of radius \(r\) with constant tangential acceleration \(a\). After time \(t\) he feels that slipping of shoes on the ground has started. The coefficient of friction between shoes and the ground is[ \(g\) \(=\) acceleration due to gravity]
363189 A child starts running from rest along a circular track of radius \(r\) with constant tangential acceleration \(a\). After time \(t\) he feels that slipping of shoes on the ground has started. The coefficient of friction between shoes and the ground is[ \(g\) \(=\) acceleration due to gravity]
363189 A child starts running from rest along a circular track of radius \(r\) with constant tangential acceleration \(a\). After time \(t\) he feels that slipping of shoes on the ground has started. The coefficient of friction between shoes and the ground is[ \(g\) \(=\) acceleration due to gravity]
363189 A child starts running from rest along a circular track of radius \(r\) with constant tangential acceleration \(a\). After time \(t\) he feels that slipping of shoes on the ground has started. The coefficient of friction between shoes and the ground is[ \(g\) \(=\) acceleration due to gravity]