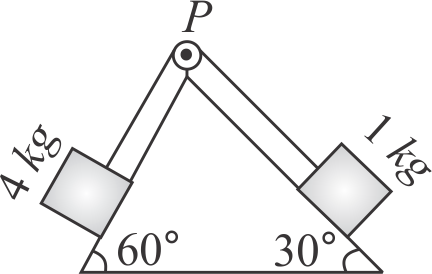
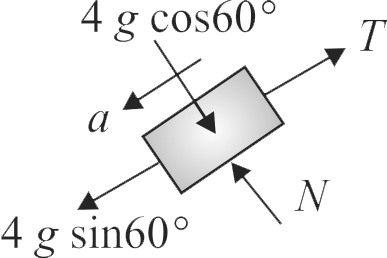
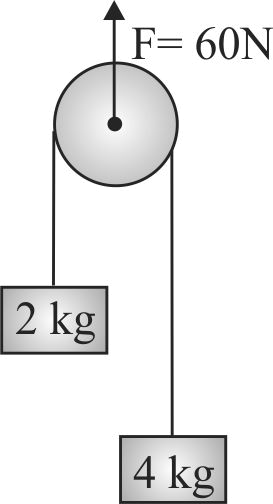
363078 At \(t=0\), the lower end of the bar \(A\) is just above the upper end of bar \(B\) (mass of bar \(A=3 {~kg}\), mass of bar \(B=\dfrac{11}{3} {~kg}\). Find time when upper end of block \(A\) just crosses the lower end of \(B\). (Assume the system was released at \(t=0)\).\(\left(g=10 {~m} / {s}^{2}\right)\)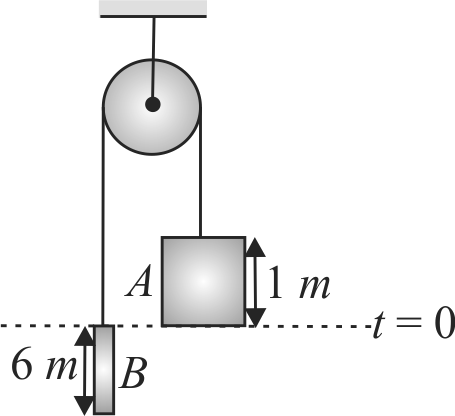

363079 As per given figure, a weightless pulley \(P\) is attached on a double inclined frictionless surfaces. The tension in the string (massless) will be (if \(g = 10\;m{\rm{/}}{s^2}\))

363080 The magnitude of relative acceleration of the two blocks is (Pulleys and threads are massless)(\(g = 10\,m/{s^2}\))

363081 A block of mass \(m\) shown in figure is in equilibrium. If it is displaced further by \(x\) and released find its acceleration just after it is released. Take pulleys to be light and smooth and strings light.

363082 In the given figure, the pulley is assumed massless and frictionless. If the friction force on the object of mass \(m\) is \(f\), then its acceleration in terms of the force \(F\) will be equal to

363078 At \(t=0\), the lower end of the bar \(A\) is just above the upper end of bar \(B\) (mass of bar \(A=3 {~kg}\), mass of bar \(B=\dfrac{11}{3} {~kg}\). Find time when upper end of block \(A\) just crosses the lower end of \(B\). (Assume the system was released at \(t=0)\).\(\left(g=10 {~m} / {s}^{2}\right)\)

363079 As per given figure, a weightless pulley \(P\) is attached on a double inclined frictionless surfaces. The tension in the string (massless) will be (if \(g = 10\;m{\rm{/}}{s^2}\))

363080 The magnitude of relative acceleration of the two blocks is (Pulleys and threads are massless)(\(g = 10\,m/{s^2}\))

363081 A block of mass \(m\) shown in figure is in equilibrium. If it is displaced further by \(x\) and released find its acceleration just after it is released. Take pulleys to be light and smooth and strings light.

363082 In the given figure, the pulley is assumed massless and frictionless. If the friction force on the object of mass \(m\) is \(f\), then its acceleration in terms of the force \(F\) will be equal to

363078 At \(t=0\), the lower end of the bar \(A\) is just above the upper end of bar \(B\) (mass of bar \(A=3 {~kg}\), mass of bar \(B=\dfrac{11}{3} {~kg}\). Find time when upper end of block \(A\) just crosses the lower end of \(B\). (Assume the system was released at \(t=0)\).\(\left(g=10 {~m} / {s}^{2}\right)\)

363079 As per given figure, a weightless pulley \(P\) is attached on a double inclined frictionless surfaces. The tension in the string (massless) will be (if \(g = 10\;m{\rm{/}}{s^2}\))

363080 The magnitude of relative acceleration of the two blocks is (Pulleys and threads are massless)(\(g = 10\,m/{s^2}\))

363081 A block of mass \(m\) shown in figure is in equilibrium. If it is displaced further by \(x\) and released find its acceleration just after it is released. Take pulleys to be light and smooth and strings light.

363082 In the given figure, the pulley is assumed massless and frictionless. If the friction force on the object of mass \(m\) is \(f\), then its acceleration in terms of the force \(F\) will be equal to

363078 At \(t=0\), the lower end of the bar \(A\) is just above the upper end of bar \(B\) (mass of bar \(A=3 {~kg}\), mass of bar \(B=\dfrac{11}{3} {~kg}\). Find time when upper end of block \(A\) just crosses the lower end of \(B\). (Assume the system was released at \(t=0)\).\(\left(g=10 {~m} / {s}^{2}\right)\)

363079 As per given figure, a weightless pulley \(P\) is attached on a double inclined frictionless surfaces. The tension in the string (massless) will be (if \(g = 10\;m{\rm{/}}{s^2}\))

363080 The magnitude of relative acceleration of the two blocks is (Pulleys and threads are massless)(\(g = 10\,m/{s^2}\))

363081 A block of mass \(m\) shown in figure is in equilibrium. If it is displaced further by \(x\) and released find its acceleration just after it is released. Take pulleys to be light and smooth and strings light.

363082 In the given figure, the pulley is assumed massless and frictionless. If the friction force on the object of mass \(m\) is \(f\), then its acceleration in terms of the force \(F\) will be equal to

363078 At \(t=0\), the lower end of the bar \(A\) is just above the upper end of bar \(B\) (mass of bar \(A=3 {~kg}\), mass of bar \(B=\dfrac{11}{3} {~kg}\). Find time when upper end of block \(A\) just crosses the lower end of \(B\). (Assume the system was released at \(t=0)\).\(\left(g=10 {~m} / {s}^{2}\right)\)

363079 As per given figure, a weightless pulley \(P\) is attached on a double inclined frictionless surfaces. The tension in the string (massless) will be (if \(g = 10\;m{\rm{/}}{s^2}\))

363080 The magnitude of relative acceleration of the two blocks is (Pulleys and threads are massless)(\(g = 10\,m/{s^2}\))

363081 A block of mass \(m\) shown in figure is in equilibrium. If it is displaced further by \(x\) and released find its acceleration just after it is released. Take pulleys to be light and smooth and strings light.

363082 In the given figure, the pulley is assumed massless and frictionless. If the friction force on the object of mass \(m\) is \(f\), then its acceleration in terms of the force \(F\) will be equal to