363029
Three point charges each of mass \(m\) and charge \(q\), are placed at the vertices of an equilateral triangle of side ' \(a\) '. \(G\) is the centroid. The system is rotated with a constant angular frequency \(\omega\) about an axis passing through the centroid and perpendicular to the plane of triangle. The ratio of magnetic dipole moment to angular momentum of the system will be :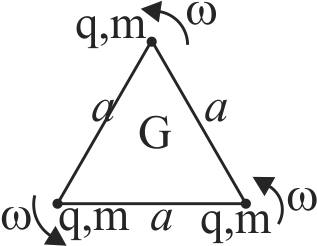
363029
Three point charges each of mass \(m\) and charge \(q\), are placed at the vertices of an equilateral triangle of side ' \(a\) '. \(G\) is the centroid. The system is rotated with a constant angular frequency \(\omega\) about an axis passing through the centroid and perpendicular to the plane of triangle. The ratio of magnetic dipole moment to angular momentum of the system will be :
363029
Three point charges each of mass \(m\) and charge \(q\), are placed at the vertices of an equilateral triangle of side ' \(a\) '. \(G\) is the centroid. The system is rotated with a constant angular frequency \(\omega\) about an axis passing through the centroid and perpendicular to the plane of triangle. The ratio of magnetic dipole moment to angular momentum of the system will be :
363029
Three point charges each of mass \(m\) and charge \(q\), are placed at the vertices of an equilateral triangle of side ' \(a\) '. \(G\) is the centroid. The system is rotated with a constant angular frequency \(\omega\) about an axis passing through the centroid and perpendicular to the plane of triangle. The ratio of magnetic dipole moment to angular momentum of the system will be :