363019 Assertion :
When radius of circular loop carrying current is doubled, its magnetic moment becomes four times.
Reason :
Magnetic moment does not depend on area of the loop.

363020 A square loop of side \(l\) carries a current \(i\). It is placed as shown in figure. The magnetic moment of the loop is

363021 In the figure shown, a coil of single turn is wound on a sphere of radius \(r\) and mass \(m\). The plane of the coil is parallel to the inclined plane and lies in the equatorial plane of the sphere. If the sphere is in rotational equlibrium, the value of \(B\) is (current in the coil is \(i\) )

363022 A wire of length ' \(L\) ' is shaped into a circle and then bent in such a way that the two semicircles are perpendicular. The magnetic moment of the system when current I flows through the system is

363023 A current \(I\) flows in a rectangulary shaped wire whose center lies at \(\left( {{x_0},0,0} \right)\) and whose vertices are located at the points \(A\left( {{x_0} + d, - a, - b} \right)\), \(B\left( {{x_0} - d,a, - b} \right),\)\(C\left( {{x_0} - d,a,b} \right),\)and \(D\left( {{x_0} + d, - a,b} \right)\) respectively. Assume that \(a,b,d < < {x_0}\). What is the magnitude of magnetic dipole vector of the rectangular wire frame? (Given : \(b = 10\,m,\) \(d = 12\,m,\) \(a = 5\,m,\) \(I = 0.03\,A\,)\)

363019 Assertion :
When radius of circular loop carrying current is doubled, its magnetic moment becomes four times.
Reason :
Magnetic moment does not depend on area of the loop.

363020 A square loop of side \(l\) carries a current \(i\). It is placed as shown in figure. The magnetic moment of the loop is

363021 In the figure shown, a coil of single turn is wound on a sphere of radius \(r\) and mass \(m\). The plane of the coil is parallel to the inclined plane and lies in the equatorial plane of the sphere. If the sphere is in rotational equlibrium, the value of \(B\) is (current in the coil is \(i\) )

363022 A wire of length ' \(L\) ' is shaped into a circle and then bent in such a way that the two semicircles are perpendicular. The magnetic moment of the system when current I flows through the system is

363023 A current \(I\) flows in a rectangulary shaped wire whose center lies at \(\left( {{x_0},0,0} \right)\) and whose vertices are located at the points \(A\left( {{x_0} + d, - a, - b} \right)\), \(B\left( {{x_0} - d,a, - b} \right),\)\(C\left( {{x_0} - d,a,b} \right),\)and \(D\left( {{x_0} + d, - a,b} \right)\) respectively. Assume that \(a,b,d < < {x_0}\). What is the magnitude of magnetic dipole vector of the rectangular wire frame? (Given : \(b = 10\,m,\) \(d = 12\,m,\) \(a = 5\,m,\) \(I = 0.03\,A\,)\)

363019 Assertion :
When radius of circular loop carrying current is doubled, its magnetic moment becomes four times.
Reason :
Magnetic moment does not depend on area of the loop.

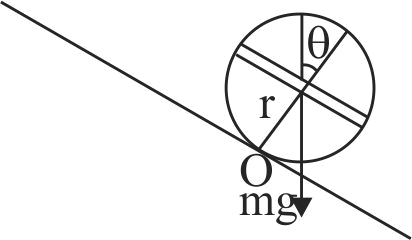
363020 A square loop of side \(l\) carries a current \(i\). It is placed as shown in figure. The magnetic moment of the loop is

363021 In the figure shown, a coil of single turn is wound on a sphere of radius \(r\) and mass \(m\). The plane of the coil is parallel to the inclined plane and lies in the equatorial plane of the sphere. If the sphere is in rotational equlibrium, the value of \(B\) is (current in the coil is \(i\) )

363022 A wire of length ' \(L\) ' is shaped into a circle and then bent in such a way that the two semicircles are perpendicular. The magnetic moment of the system when current I flows through the system is

363023 A current \(I\) flows in a rectangulary shaped wire whose center lies at \(\left( {{x_0},0,0} \right)\) and whose vertices are located at the points \(A\left( {{x_0} + d, - a, - b} \right)\), \(B\left( {{x_0} - d,a, - b} \right),\)\(C\left( {{x_0} - d,a,b} \right),\)and \(D\left( {{x_0} + d, - a,b} \right)\) respectively. Assume that \(a,b,d < < {x_0}\). What is the magnitude of magnetic dipole vector of the rectangular wire frame? (Given : \(b = 10\,m,\) \(d = 12\,m,\) \(a = 5\,m,\) \(I = 0.03\,A\,)\)

363019 Assertion :
When radius of circular loop carrying current is doubled, its magnetic moment becomes four times.
Reason :
Magnetic moment does not depend on area of the loop.

363020 A square loop of side \(l\) carries a current \(i\). It is placed as shown in figure. The magnetic moment of the loop is

363021 In the figure shown, a coil of single turn is wound on a sphere of radius \(r\) and mass \(m\). The plane of the coil is parallel to the inclined plane and lies in the equatorial plane of the sphere. If the sphere is in rotational equlibrium, the value of \(B\) is (current in the coil is \(i\) )

363022 A wire of length ' \(L\) ' is shaped into a circle and then bent in such a way that the two semicircles are perpendicular. The magnetic moment of the system when current I flows through the system is

363023 A current \(I\) flows in a rectangulary shaped wire whose center lies at \(\left( {{x_0},0,0} \right)\) and whose vertices are located at the points \(A\left( {{x_0} + d, - a, - b} \right)\), \(B\left( {{x_0} - d,a, - b} \right),\)\(C\left( {{x_0} - d,a,b} \right),\)and \(D\left( {{x_0} + d, - a,b} \right)\) respectively. Assume that \(a,b,d < < {x_0}\). What is the magnitude of magnetic dipole vector of the rectangular wire frame? (Given : \(b = 10\,m,\) \(d = 12\,m,\) \(a = 5\,m,\) \(I = 0.03\,A\,)\)

363019 Assertion :
When radius of circular loop carrying current is doubled, its magnetic moment becomes four times.
Reason :
Magnetic moment does not depend on area of the loop.

363020 A square loop of side \(l\) carries a current \(i\). It is placed as shown in figure. The magnetic moment of the loop is

363021 In the figure shown, a coil of single turn is wound on a sphere of radius \(r\) and mass \(m\). The plane of the coil is parallel to the inclined plane and lies in the equatorial plane of the sphere. If the sphere is in rotational equlibrium, the value of \(B\) is (current in the coil is \(i\) )

363022 A wire of length ' \(L\) ' is shaped into a circle and then bent in such a way that the two semicircles are perpendicular. The magnetic moment of the system when current I flows through the system is

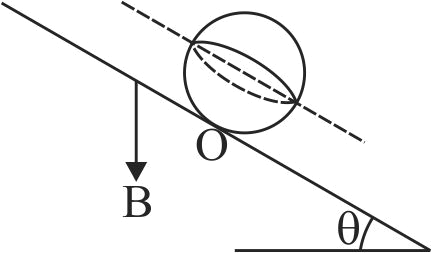
363023 A current \(I\) flows in a rectangulary shaped wire whose center lies at \(\left( {{x_0},0,0} \right)\) and whose vertices are located at the points \(A\left( {{x_0} + d, - a, - b} \right)\), \(B\left( {{x_0} - d,a, - b} \right),\)\(C\left( {{x_0} - d,a,b} \right),\)and \(D\left( {{x_0} + d, - a,b} \right)\) respectively. Assume that \(a,b,d < < {x_0}\). What is the magnitude of magnetic dipole vector of the rectangular wire frame? (Given : \(b = 10\,m,\) \(d = 12\,m,\) \(a = 5\,m,\) \(I = 0.03\,A\,)\)