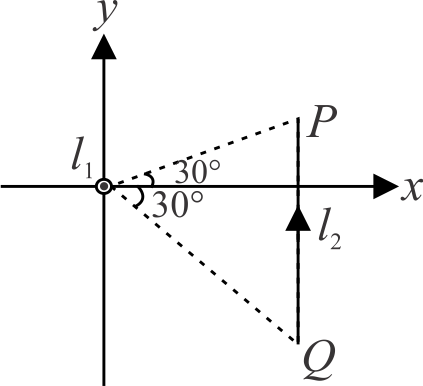362698
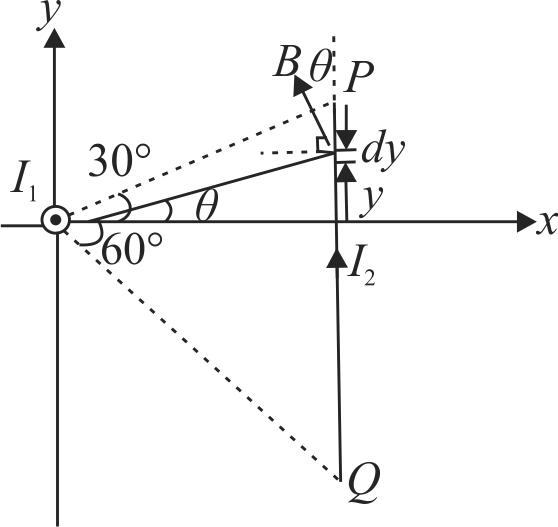
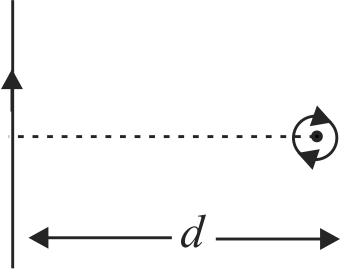
An infinite wire, placed along \({z}\)-axis, has current \({I_{I}}\) in positive \({z}\)-direction. A conducting rod \({P Q}\) placed in \({x y}\) plane parallel to \({y}\)-axis has current \({I_{2}}\) in positive \({y}\)-direction. The ends of the rod subtend angles \({30^{\circ}}\) and \({60^{\circ}}\) at the origin with positive \({x}\)-direction as shown in figure. The rod is at a distance \({a}\) from the origin. If the net force on the rod is found to be \({\dfrac{\mu_{0} I_{1} I_{2}}{4 \pi} \ln N}\), find the value of \({N}\).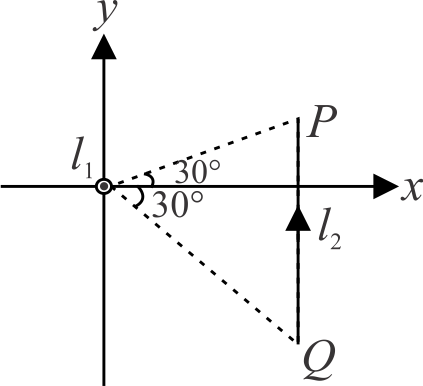
362698
An infinite wire, placed along \({z}\)-axis, has current \({I_{I}}\) in positive \({z}\)-direction. A conducting rod \({P Q}\) placed in \({x y}\) plane parallel to \({y}\)-axis has current \({I_{2}}\) in positive \({y}\)-direction. The ends of the rod subtend angles \({30^{\circ}}\) and \({60^{\circ}}\) at the origin with positive \({x}\)-direction as shown in figure. The rod is at a distance \({a}\) from the origin. If the net force on the rod is found to be \({\dfrac{\mu_{0} I_{1} I_{2}}{4 \pi} \ln N}\), find the value of \({N}\).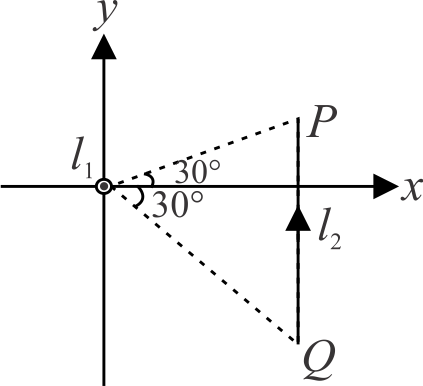
362698
An infinite wire, placed along \({z}\)-axis, has current \({I_{I}}\) in positive \({z}\)-direction. A conducting rod \({P Q}\) placed in \({x y}\) plane parallel to \({y}\)-axis has current \({I_{2}}\) in positive \({y}\)-direction. The ends of the rod subtend angles \({30^{\circ}}\) and \({60^{\circ}}\) at the origin with positive \({x}\)-direction as shown in figure. The rod is at a distance \({a}\) from the origin. If the net force on the rod is found to be \({\dfrac{\mu_{0} I_{1} I_{2}}{4 \pi} \ln N}\), find the value of \({N}\).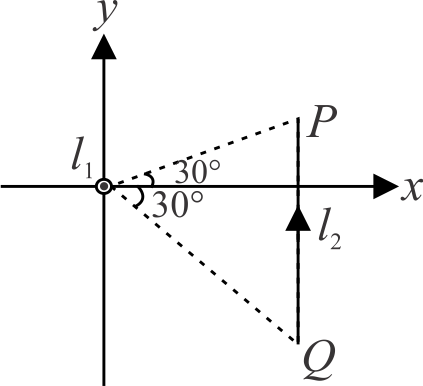
362698
An infinite wire, placed along \({z}\)-axis, has current \({I_{I}}\) in positive \({z}\)-direction. A conducting rod \({P Q}\) placed in \({x y}\) plane parallel to \({y}\)-axis has current \({I_{2}}\) in positive \({y}\)-direction. The ends of the rod subtend angles \({30^{\circ}}\) and \({60^{\circ}}\) at the origin with positive \({x}\)-direction as shown in figure. The rod is at a distance \({a}\) from the origin. If the net force on the rod is found to be \({\dfrac{\mu_{0} I_{1} I_{2}}{4 \pi} \ln N}\), find the value of \({N}\).