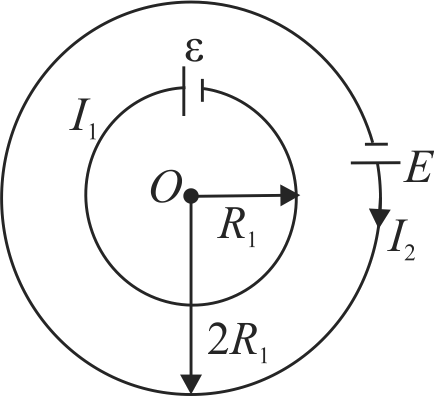
362557 Two coplanar concentric circular wires made of same material have radius \({R_{1}}\) and \({R_{2}\left(=2 R_{1}\right)}\). The wires carry current due to identical source of emf having no internal resistance. Find the ratio of radii of cross section of the two wires \(\left( {\left. {\frac{{{r_1}}}{{{r_2}}} = ?} \right)} \right.\) if the magnetic induction field at the centre of the circle is zero.
362560
Three rings, each having equal radius \(R\), are placed mutually perpendicular to each other and each having its center at the origin of coordinate system. If a current \(I\) is flowing through each ring, then the magnitude of the magnetic field at the common center is: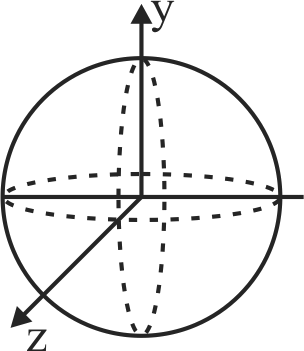
362557 Two coplanar concentric circular wires made of same material have radius \({R_{1}}\) and \({R_{2}\left(=2 R_{1}\right)}\). The wires carry current due to identical source of emf having no internal resistance. Find the ratio of radii of cross section of the two wires \(\left( {\left. {\frac{{{r_1}}}{{{r_2}}} = ?} \right)} \right.\) if the magnetic induction field at the centre of the circle is zero.
362560
Three rings, each having equal radius \(R\), are placed mutually perpendicular to each other and each having its center at the origin of coordinate system. If a current \(I\) is flowing through each ring, then the magnitude of the magnetic field at the common center is:
362557 Two coplanar concentric circular wires made of same material have radius \({R_{1}}\) and \({R_{2}\left(=2 R_{1}\right)}\). The wires carry current due to identical source of emf having no internal resistance. Find the ratio of radii of cross section of the two wires \(\left( {\left. {\frac{{{r_1}}}{{{r_2}}} = ?} \right)} \right.\) if the magnetic induction field at the centre of the circle is zero.
362560
Three rings, each having equal radius \(R\), are placed mutually perpendicular to each other and each having its center at the origin of coordinate system. If a current \(I\) is flowing through each ring, then the magnitude of the magnetic field at the common center is:
362557 Two coplanar concentric circular wires made of same material have radius \({R_{1}}\) and \({R_{2}\left(=2 R_{1}\right)}\). The wires carry current due to identical source of emf having no internal resistance. Find the ratio of radii of cross section of the two wires \(\left( {\left. {\frac{{{r_1}}}{{{r_2}}} = ?} \right)} \right.\) if the magnetic induction field at the centre of the circle is zero.
362560
Three rings, each having equal radius \(R\), are placed mutually perpendicular to each other and each having its center at the origin of coordinate system. If a current \(I\) is flowing through each ring, then the magnitude of the magnetic field at the common center is: