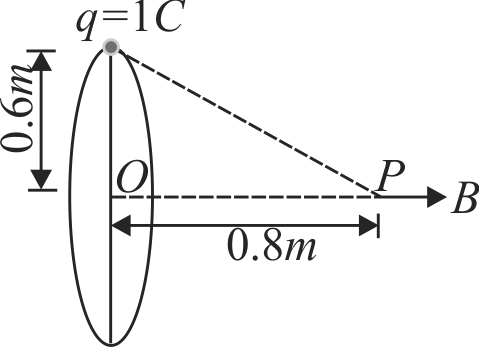
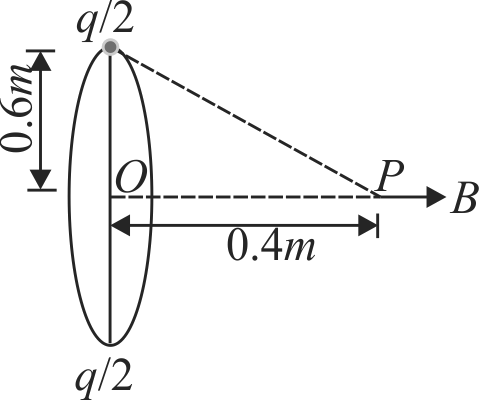
362629 A charge of 1\(C\) is placed at one end of a conducting rod of length 0.6\(m\). The rod is rotated in a vertical plane about a horizontal axis passing through the other end of the rod with angular frequency \(10^{4} \pi \mathrm{rads}^{-1}\). The magnetic field at a point on the axis of rotation at a distance of \(0.8 m\) from the centre of the path is \(B_{1}\). Now, half of the charge is removed from one end and placed on the other end. The rod is rotated in a vertical plane about a horizontal axis passing through the midpoint of the rod with same angular frequency. The magnetic field at a point on the axis at a distance of 0.4\(m\) from the centre of the rod is \(B_{2}\) then \(\dfrac{B_{2}}{B_{1}}=\)
362629 A charge of 1\(C\) is placed at one end of a conducting rod of length 0.6\(m\). The rod is rotated in a vertical plane about a horizontal axis passing through the other end of the rod with angular frequency \(10^{4} \pi \mathrm{rads}^{-1}\). The magnetic field at a point on the axis of rotation at a distance of \(0.8 m\) from the centre of the path is \(B_{1}\). Now, half of the charge is removed from one end and placed on the other end. The rod is rotated in a vertical plane about a horizontal axis passing through the midpoint of the rod with same angular frequency. The magnetic field at a point on the axis at a distance of 0.4\(m\) from the centre of the rod is \(B_{2}\) then \(\dfrac{B_{2}}{B_{1}}=\)
362629 A charge of 1\(C\) is placed at one end of a conducting rod of length 0.6\(m\). The rod is rotated in a vertical plane about a horizontal axis passing through the other end of the rod with angular frequency \(10^{4} \pi \mathrm{rads}^{-1}\). The magnetic field at a point on the axis of rotation at a distance of \(0.8 m\) from the centre of the path is \(B_{1}\). Now, half of the charge is removed from one end and placed on the other end. The rod is rotated in a vertical plane about a horizontal axis passing through the midpoint of the rod with same angular frequency. The magnetic field at a point on the axis at a distance of 0.4\(m\) from the centre of the rod is \(B_{2}\) then \(\dfrac{B_{2}}{B_{1}}=\)
362629 A charge of 1\(C\) is placed at one end of a conducting rod of length 0.6\(m\). The rod is rotated in a vertical plane about a horizontal axis passing through the other end of the rod with angular frequency \(10^{4} \pi \mathrm{rads}^{-1}\). The magnetic field at a point on the axis of rotation at a distance of \(0.8 m\) from the centre of the path is \(B_{1}\). Now, half of the charge is removed from one end and placed on the other end. The rod is rotated in a vertical plane about a horizontal axis passing through the midpoint of the rod with same angular frequency. The magnetic field at a point on the axis at a distance of 0.4\(m\) from the centre of the rod is \(B_{2}\) then \(\dfrac{B_{2}}{B_{1}}=\)