362536
Figure shows a coil of radius \(2\;cm\) concentricwith a coil of radius \(4\;cm\). Each coil has 1000 turns with a current of \(5\,amp\). In larger coil, then the current needed in the smaller coil to give the total magnetic field at the centre equal to \(2\;mT\) is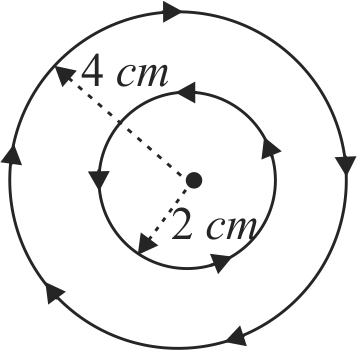
362538 A wire of finite length carries a steady current. It is first bent to form a circular coil of one turn. The same length is now bent more sharply to give a loop of two turns of smaller radius. The magnetic field at the centre caused by the same current now will be
362536
Figure shows a coil of radius \(2\;cm\) concentricwith a coil of radius \(4\;cm\). Each coil has 1000 turns with a current of \(5\,amp\). In larger coil, then the current needed in the smaller coil to give the total magnetic field at the centre equal to \(2\;mT\) is
362538 A wire of finite length carries a steady current. It is first bent to form a circular coil of one turn. The same length is now bent more sharply to give a loop of two turns of smaller radius. The magnetic field at the centre caused by the same current now will be
362536
Figure shows a coil of radius \(2\;cm\) concentricwith a coil of radius \(4\;cm\). Each coil has 1000 turns with a current of \(5\,amp\). In larger coil, then the current needed in the smaller coil to give the total magnetic field at the centre equal to \(2\;mT\) is
362538 A wire of finite length carries a steady current. It is first bent to form a circular coil of one turn. The same length is now bent more sharply to give a loop of two turns of smaller radius. The magnetic field at the centre caused by the same current now will be
362536
Figure shows a coil of radius \(2\;cm\) concentricwith a coil of radius \(4\;cm\). Each coil has 1000 turns with a current of \(5\,amp\). In larger coil, then the current needed in the smaller coil to give the total magnetic field at the centre equal to \(2\;mT\) is
362538 A wire of finite length carries a steady current. It is first bent to form a circular coil of one turn. The same length is now bent more sharply to give a loop of two turns of smaller radius. The magnetic field at the centre caused by the same current now will be