362486
A long, straight, hollow conductor (tube) carrying a current has two sections \(A\) and \(C\) of unequal cross- section joined by a conical section \(B\). 1, 2 and 3 are points on a line parallel to the axis of the conductor. The magnetic field at 1,2 and 3 have magnitudes \(B_{1}, B_{2}\) and \(B_{3}\) :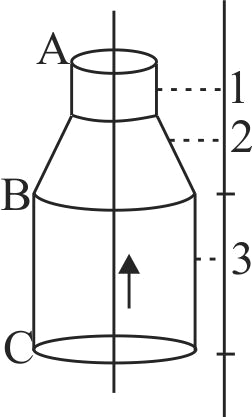
362487
Figure shows an amperian path \(ABCDA\). Part \(ABC\) is in vertical plane \(PSTU\) while part \(CDA\) is in horizontal plane \(PQRS\). Direction of circulation along the path is shown by an arrow near point \(B\) and at \(D\). \(\oint \vec{B} \cdot d \vec{l}\) for this path according to Ampere's law will be: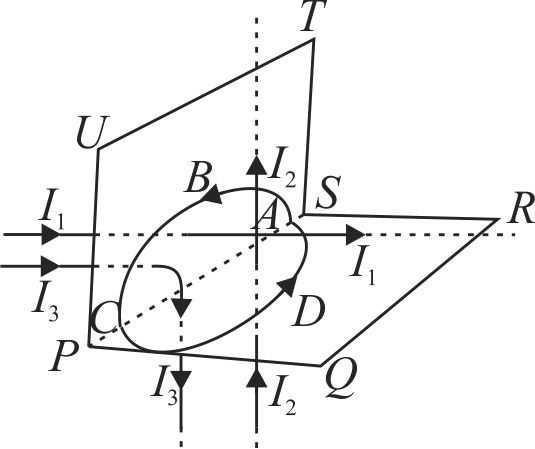
362488
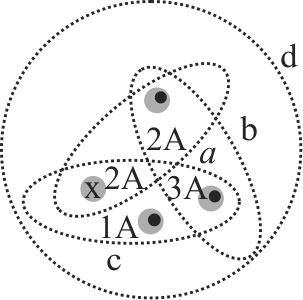
Six very long insulated copper wires are bound
together to form a cable. The currents carried by the wires are
\({I_1} = + 10\;A,{I_2} = - 13\;A,{\rm{ }}{I_3} = + 10\;A,{I_4}\)
\( = + 7\;A,{I_5} = - 12\;A,{I_6} = + 18\;A\),
The magnetic induction at a perpendicular
distance of 10\(cm\) from the cable is
\(\left( {{\mu _0} = 4\pi \times {{10}^{ - 7}}\;Wb/A - m} \right)\)
362489
Five very long, straight, insulated wires are closely bound together to form a small cable. Currents carried by the wires are:
\({I_1} = 20\;A,{I_2} = - 6\;A,{I_3} = 12\;A,{I_4} = - 7\;A,{\rm{ }}{I_5} = 18\;A\). [Negative currents are opposite in direction to the positive]. The magnetic field induction at a distance of \(10 \mathrm{~cm}\) from the cable is
362486
A long, straight, hollow conductor (tube) carrying a current has two sections \(A\) and \(C\) of unequal cross- section joined by a conical section \(B\). 1, 2 and 3 are points on a line parallel to the axis of the conductor. The magnetic field at 1,2 and 3 have magnitudes \(B_{1}, B_{2}\) and \(B_{3}\) :
362487
Figure shows an amperian path \(ABCDA\). Part \(ABC\) is in vertical plane \(PSTU\) while part \(CDA\) is in horizontal plane \(PQRS\). Direction of circulation along the path is shown by an arrow near point \(B\) and at \(D\). \(\oint \vec{B} \cdot d \vec{l}\) for this path according to Ampere's law will be:
362488
Six very long insulated copper wires are bound
together to form a cable. The currents carried by the wires are
\({I_1} = + 10\;A,{I_2} = - 13\;A,{\rm{ }}{I_3} = + 10\;A,{I_4}\)
\( = + 7\;A,{I_5} = - 12\;A,{I_6} = + 18\;A\),
The magnetic induction at a perpendicular
distance of 10\(cm\) from the cable is
\(\left( {{\mu _0} = 4\pi \times {{10}^{ - 7}}\;Wb/A - m} \right)\)
362489
Five very long, straight, insulated wires are closely bound together to form a small cable. Currents carried by the wires are:
\({I_1} = 20\;A,{I_2} = - 6\;A,{I_3} = 12\;A,{I_4} = - 7\;A,{\rm{ }}{I_5} = 18\;A\). [Negative currents are opposite in direction to the positive]. The magnetic field induction at a distance of \(10 \mathrm{~cm}\) from the cable is
362486
A long, straight, hollow conductor (tube) carrying a current has two sections \(A\) and \(C\) of unequal cross- section joined by a conical section \(B\). 1, 2 and 3 are points on a line parallel to the axis of the conductor. The magnetic field at 1,2 and 3 have magnitudes \(B_{1}, B_{2}\) and \(B_{3}\) :
362487
Figure shows an amperian path \(ABCDA\). Part \(ABC\) is in vertical plane \(PSTU\) while part \(CDA\) is in horizontal plane \(PQRS\). Direction of circulation along the path is shown by an arrow near point \(B\) and at \(D\). \(\oint \vec{B} \cdot d \vec{l}\) for this path according to Ampere's law will be:
362488
Six very long insulated copper wires are bound
together to form a cable. The currents carried by the wires are
\({I_1} = + 10\;A,{I_2} = - 13\;A,{\rm{ }}{I_3} = + 10\;A,{I_4}\)
\( = + 7\;A,{I_5} = - 12\;A,{I_6} = + 18\;A\),
The magnetic induction at a perpendicular
distance of 10\(cm\) from the cable is
\(\left( {{\mu _0} = 4\pi \times {{10}^{ - 7}}\;Wb/A - m} \right)\)
362489
Five very long, straight, insulated wires are closely bound together to form a small cable. Currents carried by the wires are:
\({I_1} = 20\;A,{I_2} = - 6\;A,{I_3} = 12\;A,{I_4} = - 7\;A,{\rm{ }}{I_5} = 18\;A\). [Negative currents are opposite in direction to the positive]. The magnetic field induction at a distance of \(10 \mathrm{~cm}\) from the cable is
362486
A long, straight, hollow conductor (tube) carrying a current has two sections \(A\) and \(C\) of unequal cross- section joined by a conical section \(B\). 1, 2 and 3 are points on a line parallel to the axis of the conductor. The magnetic field at 1,2 and 3 have magnitudes \(B_{1}, B_{2}\) and \(B_{3}\) :
362487
Figure shows an amperian path \(ABCDA\). Part \(ABC\) is in vertical plane \(PSTU\) while part \(CDA\) is in horizontal plane \(PQRS\). Direction of circulation along the path is shown by an arrow near point \(B\) and at \(D\). \(\oint \vec{B} \cdot d \vec{l}\) for this path according to Ampere's law will be:
362488
Six very long insulated copper wires are bound
together to form a cable. The currents carried by the wires are
\({I_1} = + 10\;A,{I_2} = - 13\;A,{\rm{ }}{I_3} = + 10\;A,{I_4}\)
\( = + 7\;A,{I_5} = - 12\;A,{I_6} = + 18\;A\),
The magnetic induction at a perpendicular
distance of 10\(cm\) from the cable is
\(\left( {{\mu _0} = 4\pi \times {{10}^{ - 7}}\;Wb/A - m} \right)\)
362489
Five very long, straight, insulated wires are closely bound together to form a small cable. Currents carried by the wires are:
\({I_1} = 20\;A,{I_2} = - 6\;A,{I_3} = 12\;A,{I_4} = - 7\;A,{\rm{ }}{I_5} = 18\;A\). [Negative currents are opposite in direction to the positive]. The magnetic field induction at a distance of \(10 \mathrm{~cm}\) from the cable is
362486
A long, straight, hollow conductor (tube) carrying a current has two sections \(A\) and \(C\) of unequal cross- section joined by a conical section \(B\). 1, 2 and 3 are points on a line parallel to the axis of the conductor. The magnetic field at 1,2 and 3 have magnitudes \(B_{1}, B_{2}\) and \(B_{3}\) :
362487
Figure shows an amperian path \(ABCDA\). Part \(ABC\) is in vertical plane \(PSTU\) while part \(CDA\) is in horizontal plane \(PQRS\). Direction of circulation along the path is shown by an arrow near point \(B\) and at \(D\). \(\oint \vec{B} \cdot d \vec{l}\) for this path according to Ampere's law will be:
362488
Six very long insulated copper wires are bound
together to form a cable. The currents carried by the wires are
\({I_1} = + 10\;A,{I_2} = - 13\;A,{\rm{ }}{I_3} = + 10\;A,{I_4}\)
\( = + 7\;A,{I_5} = - 12\;A,{I_6} = + 18\;A\),
The magnetic induction at a perpendicular
distance of 10\(cm\) from the cable is
\(\left( {{\mu _0} = 4\pi \times {{10}^{ - 7}}\;Wb/A - m} \right)\)
362489
Five very long, straight, insulated wires are closely bound together to form a small cable. Currents carried by the wires are:
\({I_1} = 20\;A,{I_2} = - 6\;A,{I_3} = 12\;A,{I_4} = - 7\;A,{\rm{ }}{I_5} = 18\;A\). [Negative currents are opposite in direction to the positive]. The magnetic field induction at a distance of \(10 \mathrm{~cm}\) from the cable is