Explanation:
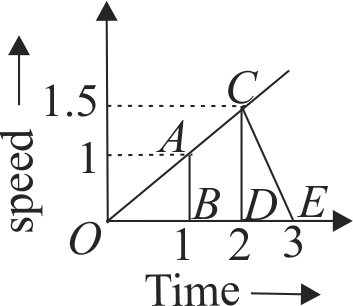
Distance travelled by the particle ,
\(s=\) Area under the curve
\(=s_{01}+s_{12}+s_{23}\)
\(s=\) Area of \(\triangle O A B\)
+ Area of trapezium A B C D
\(\quad + {\rm{Area}}\,\,{\rm{of}}\,\,\Delta DCE\)
\( = \frac{1}{2} \times OB \times AB + \frac{1}{2}(AB + CD) \times BD + \frac{1}{2}\)
\( \times DE \times DC\)
\( = \frac{1}{2} \times \left( {1 - 0} \right) \times 1 + \frac{1}{2} \times \left( {1 + 1.5} \right) \times \left( {2 - 1} \right)\)
\( + \frac{1}{2} \times \left( {3 - 2} \right) \times 1.5\)
\( = \frac{1}{2} + \frac{1}{2} \times 2.5 + \frac{1}{2} \times 1.5\)
[ \(\because \) area of triangle \( = \,\,\frac{1}{2}\,\,\, \times \) base \(\,\, \times \,\,\)height]
\({\rm{area}}\,\,{\rm{of}}\,\,{\rm{trapezium}} = \frac{1}{2} \times \)
\(\left( {{\rm{sum}}} \right.{\rm{of}}\left. {\left. {{\rm{parallel}}\,\,{\rm{sides}}} \right) \times {\rm{height}}} \right]\)
\( = \frac{1}{2}\left( {1 + 2.5 + 1.5} \right) = \frac{1}{2} \times 5 = \frac{5}{2}m\)