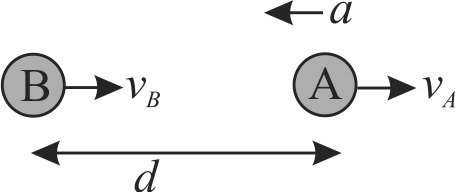
362308 Two cars \(A\) and \(B\) are travelling in the same direction with velocities \({v_{\rm{A}}}\,{\rm{and}}\,{v_B}\left( {{v_{\rm{A}}} > {v_{\rm{B}}}} \right)\). The initial seperation between the cars is \(d\). When the car \(A\) applies brakes producing a uniform retardation \(a\). There will be no collision when
362308 Two cars \(A\) and \(B\) are travelling in the same direction with velocities \({v_{\rm{A}}}\,{\rm{and}}\,{v_B}\left( {{v_{\rm{A}}} > {v_{\rm{B}}}} \right)\). The initial seperation between the cars is \(d\). When the car \(A\) applies brakes producing a uniform retardation \(a\). There will be no collision when
362308 Two cars \(A\) and \(B\) are travelling in the same direction with velocities \({v_{\rm{A}}}\,{\rm{and}}\,{v_B}\left( {{v_{\rm{A}}} > {v_{\rm{B}}}} \right)\). The initial seperation between the cars is \(d\). When the car \(A\) applies brakes producing a uniform retardation \(a\). There will be no collision when
362308 Two cars \(A\) and \(B\) are travelling in the same direction with velocities \({v_{\rm{A}}}\,{\rm{and}}\,{v_B}\left( {{v_{\rm{A}}} > {v_{\rm{B}}}} \right)\). The initial seperation between the cars is \(d\). When the car \(A\) applies brakes producing a uniform retardation \(a\). There will be no collision when
362308 Two cars \(A\) and \(B\) are travelling in the same direction with velocities \({v_{\rm{A}}}\,{\rm{and}}\,{v_B}\left( {{v_{\rm{A}}} > {v_{\rm{B}}}} \right)\). The initial seperation between the cars is \(d\). When the car \(A\) applies brakes producing a uniform retardation \(a\). There will be no collision when