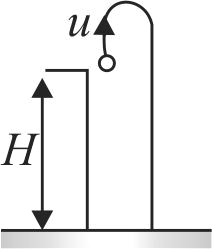
362337 A horizontal bridge is built across a river. A student standing on the bridge throws a small ball vertically upwards with a velocity \(4\,\,m{s^{ - 1}}.\)The ball strikes the water surface after \(4{\rm{ }}s\). The height of bridge above water surface is ( Take \(g = 10\,m{s^{ - 2}}\))
362338
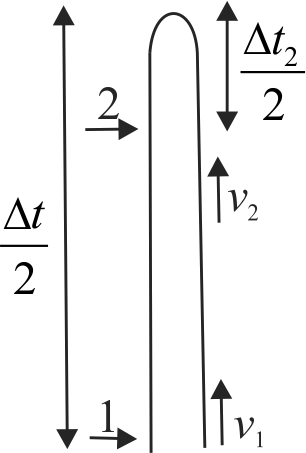
The figure shows a method for measuring the acceleration due to gravity. The ball is projected upward by a "gun". The ball passes electronic "gates" 1 and 2 as it rises and again as it falls. Each gate is connected to a separate timer. The first passage of the ball through each gate starts the corresponding timer, and the second passage through the same gate stops the timer. The time intervals \(\Delta t_{1}\) and \(\Delta t_{2}\) are thus measured. The vertical distance between the two gates is \(d\). If \(d=5 {~m}\), \(\Delta t_{1}=3 {~s}, \Delta t_{2}=2 {~s}\), find the measured value of acceleration due to gravity.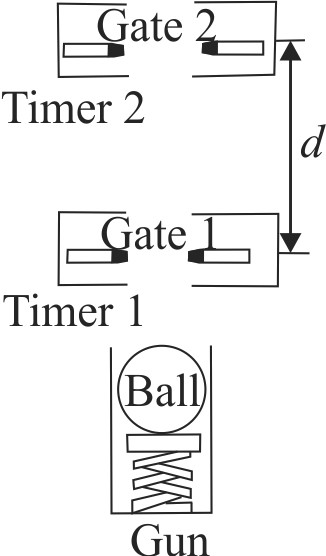
362337 A horizontal bridge is built across a river. A student standing on the bridge throws a small ball vertically upwards with a velocity \(4\,\,m{s^{ - 1}}.\)The ball strikes the water surface after \(4{\rm{ }}s\). The height of bridge above water surface is ( Take \(g = 10\,m{s^{ - 2}}\))
362338
The figure shows a method for measuring the acceleration due to gravity. The ball is projected upward by a "gun". The ball passes electronic "gates" 1 and 2 as it rises and again as it falls. Each gate is connected to a separate timer. The first passage of the ball through each gate starts the corresponding timer, and the second passage through the same gate stops the timer. The time intervals \(\Delta t_{1}\) and \(\Delta t_{2}\) are thus measured. The vertical distance between the two gates is \(d\). If \(d=5 {~m}\), \(\Delta t_{1}=3 {~s}, \Delta t_{2}=2 {~s}\), find the measured value of acceleration due to gravity.
362337 A horizontal bridge is built across a river. A student standing on the bridge throws a small ball vertically upwards with a velocity \(4\,\,m{s^{ - 1}}.\)The ball strikes the water surface after \(4{\rm{ }}s\). The height of bridge above water surface is ( Take \(g = 10\,m{s^{ - 2}}\))
362338
The figure shows a method for measuring the acceleration due to gravity. The ball is projected upward by a "gun". The ball passes electronic "gates" 1 and 2 as it rises and again as it falls. Each gate is connected to a separate timer. The first passage of the ball through each gate starts the corresponding timer, and the second passage through the same gate stops the timer. The time intervals \(\Delta t_{1}\) and \(\Delta t_{2}\) are thus measured. The vertical distance between the two gates is \(d\). If \(d=5 {~m}\), \(\Delta t_{1}=3 {~s}, \Delta t_{2}=2 {~s}\), find the measured value of acceleration due to gravity.
362337 A horizontal bridge is built across a river. A student standing on the bridge throws a small ball vertically upwards with a velocity \(4\,\,m{s^{ - 1}}.\)The ball strikes the water surface after \(4{\rm{ }}s\). The height of bridge above water surface is ( Take \(g = 10\,m{s^{ - 2}}\))
362338
The figure shows a method for measuring the acceleration due to gravity. The ball is projected upward by a "gun". The ball passes electronic "gates" 1 and 2 as it rises and again as it falls. Each gate is connected to a separate timer. The first passage of the ball through each gate starts the corresponding timer, and the second passage through the same gate stops the timer. The time intervals \(\Delta t_{1}\) and \(\Delta t_{2}\) are thus measured. The vertical distance between the two gates is \(d\). If \(d=5 {~m}\), \(\Delta t_{1}=3 {~s}, \Delta t_{2}=2 {~s}\), find the measured value of acceleration due to gravity.
362337 A horizontal bridge is built across a river. A student standing on the bridge throws a small ball vertically upwards with a velocity \(4\,\,m{s^{ - 1}}.\)The ball strikes the water surface after \(4{\rm{ }}s\). The height of bridge above water surface is ( Take \(g = 10\,m{s^{ - 2}}\))
362338
The figure shows a method for measuring the acceleration due to gravity. The ball is projected upward by a "gun". The ball passes electronic "gates" 1 and 2 as it rises and again as it falls. Each gate is connected to a separate timer. The first passage of the ball through each gate starts the corresponding timer, and the second passage through the same gate stops the timer. The time intervals \(\Delta t_{1}\) and \(\Delta t_{2}\) are thus measured. The vertical distance between the two gates is \(d\). If \(d=5 {~m}\), \(\Delta t_{1}=3 {~s}, \Delta t_{2}=2 {~s}\), find the measured value of acceleration due to gravity.