362113
Two towers \(A B\) and \(C D\) are situated at distance \(d\) apart as shown in figure. \(A B\) is 20 \(m\) high and \(C D\) is 30 \(m\) high from the ground. A particle is thrown from the top of \(A B\) horizontally with a velocity of \(10 {~ms}^{-1}\) towards \(C D\). Simultaneously, another particle is thrown from the top of \(C D\) at an angle \(60^{\circ}\) to the horizontal towards \(A B\) with the same magnitude of initial velocity as that of the first object. The two particles move in the same vertical plane, collide in mid-air, calculate the distance \(d\) between the towers.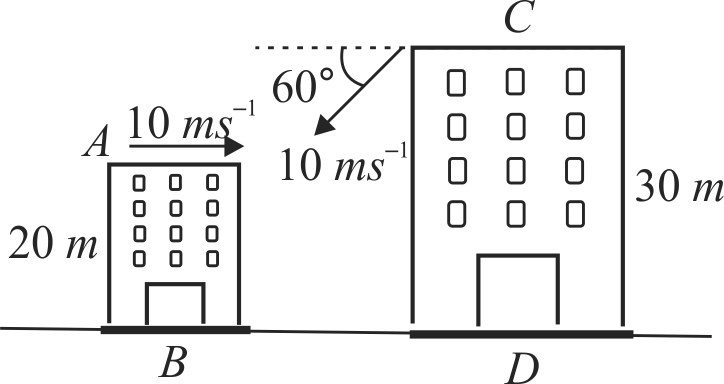
362115
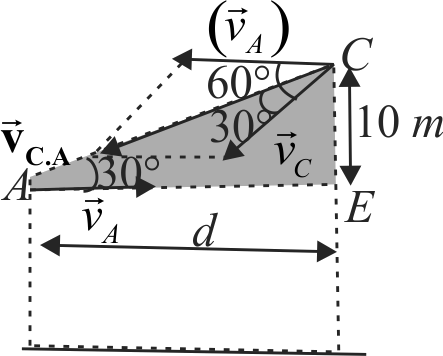
A projectile \(A\) is thrown at an angle \(30^{\circ}\) to the horizontal from point \(P\). At the same time, another projectile \(B\) is thrown with velocity \(v_{2}\) upwards from the point \(Q\) vertically below the highest point. For \(B\) to collide with \(A, \dfrac{v_{2}}{v_{1}}\) should be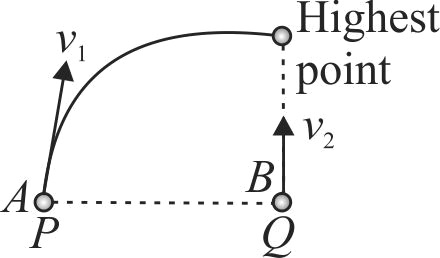
362116
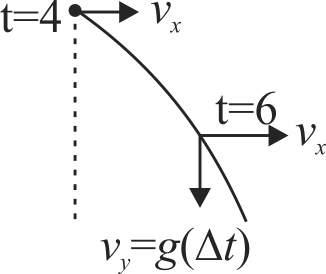
A train is moving along a straight line with a constant acceleration a. A boy standing in the train throws a ball forward with a speed of \(6\;m{\rm{/}}s\) at an angle of \(30^{\circ}\) to the horizontal. The boy has to move forward by \(2.5\;m\) inside the train to catch the ball back at the initial height. The acceleration of the train is
(Take \(\sqrt 3 = 1.73,g = 10\;m{\rm{/}}{{\rm{s}}^2}\))
362113
Two towers \(A B\) and \(C D\) are situated at distance \(d\) apart as shown in figure. \(A B\) is 20 \(m\) high and \(C D\) is 30 \(m\) high from the ground. A particle is thrown from the top of \(A B\) horizontally with a velocity of \(10 {~ms}^{-1}\) towards \(C D\). Simultaneously, another particle is thrown from the top of \(C D\) at an angle \(60^{\circ}\) to the horizontal towards \(A B\) with the same magnitude of initial velocity as that of the first object. The two particles move in the same vertical plane, collide in mid-air, calculate the distance \(d\) between the towers.
362115
A projectile \(A\) is thrown at an angle \(30^{\circ}\) to the horizontal from point \(P\). At the same time, another projectile \(B\) is thrown with velocity \(v_{2}\) upwards from the point \(Q\) vertically below the highest point. For \(B\) to collide with \(A, \dfrac{v_{2}}{v_{1}}\) should be
362116
A train is moving along a straight line with a constant acceleration a. A boy standing in the train throws a ball forward with a speed of \(6\;m{\rm{/}}s\) at an angle of \(30^{\circ}\) to the horizontal. The boy has to move forward by \(2.5\;m\) inside the train to catch the ball back at the initial height. The acceleration of the train is
(Take \(\sqrt 3 = 1.73,g = 10\;m{\rm{/}}{{\rm{s}}^2}\))
362113
Two towers \(A B\) and \(C D\) are situated at distance \(d\) apart as shown in figure. \(A B\) is 20 \(m\) high and \(C D\) is 30 \(m\) high from the ground. A particle is thrown from the top of \(A B\) horizontally with a velocity of \(10 {~ms}^{-1}\) towards \(C D\). Simultaneously, another particle is thrown from the top of \(C D\) at an angle \(60^{\circ}\) to the horizontal towards \(A B\) with the same magnitude of initial velocity as that of the first object. The two particles move in the same vertical plane, collide in mid-air, calculate the distance \(d\) between the towers.
362115
A projectile \(A\) is thrown at an angle \(30^{\circ}\) to the horizontal from point \(P\). At the same time, another projectile \(B\) is thrown with velocity \(v_{2}\) upwards from the point \(Q\) vertically below the highest point. For \(B\) to collide with \(A, \dfrac{v_{2}}{v_{1}}\) should be
362116
A train is moving along a straight line with a constant acceleration a. A boy standing in the train throws a ball forward with a speed of \(6\;m{\rm{/}}s\) at an angle of \(30^{\circ}\) to the horizontal. The boy has to move forward by \(2.5\;m\) inside the train to catch the ball back at the initial height. The acceleration of the train is
(Take \(\sqrt 3 = 1.73,g = 10\;m{\rm{/}}{{\rm{s}}^2}\))
362113
Two towers \(A B\) and \(C D\) are situated at distance \(d\) apart as shown in figure. \(A B\) is 20 \(m\) high and \(C D\) is 30 \(m\) high from the ground. A particle is thrown from the top of \(A B\) horizontally with a velocity of \(10 {~ms}^{-1}\) towards \(C D\). Simultaneously, another particle is thrown from the top of \(C D\) at an angle \(60^{\circ}\) to the horizontal towards \(A B\) with the same magnitude of initial velocity as that of the first object. The two particles move in the same vertical plane, collide in mid-air, calculate the distance \(d\) between the towers.
362115
A projectile \(A\) is thrown at an angle \(30^{\circ}\) to the horizontal from point \(P\). At the same time, another projectile \(B\) is thrown with velocity \(v_{2}\) upwards from the point \(Q\) vertically below the highest point. For \(B\) to collide with \(A, \dfrac{v_{2}}{v_{1}}\) should be
362116
A train is moving along a straight line with a constant acceleration a. A boy standing in the train throws a ball forward with a speed of \(6\;m{\rm{/}}s\) at an angle of \(30^{\circ}\) to the horizontal. The boy has to move forward by \(2.5\;m\) inside the train to catch the ball back at the initial height. The acceleration of the train is
(Take \(\sqrt 3 = 1.73,g = 10\;m{\rm{/}}{{\rm{s}}^2}\))
362113
Two towers \(A B\) and \(C D\) are situated at distance \(d\) apart as shown in figure. \(A B\) is 20 \(m\) high and \(C D\) is 30 \(m\) high from the ground. A particle is thrown from the top of \(A B\) horizontally with a velocity of \(10 {~ms}^{-1}\) towards \(C D\). Simultaneously, another particle is thrown from the top of \(C D\) at an angle \(60^{\circ}\) to the horizontal towards \(A B\) with the same magnitude of initial velocity as that of the first object. The two particles move in the same vertical plane, collide in mid-air, calculate the distance \(d\) between the towers.
362115
A projectile \(A\) is thrown at an angle \(30^{\circ}\) to the horizontal from point \(P\). At the same time, another projectile \(B\) is thrown with velocity \(v_{2}\) upwards from the point \(Q\) vertically below the highest point. For \(B\) to collide with \(A, \dfrac{v_{2}}{v_{1}}\) should be
362116
A train is moving along a straight line with a constant acceleration a. A boy standing in the train throws a ball forward with a speed of \(6\;m{\rm{/}}s\) at an angle of \(30^{\circ}\) to the horizontal. The boy has to move forward by \(2.5\;m\) inside the train to catch the ball back at the initial height. The acceleration of the train is
(Take \(\sqrt 3 = 1.73,g = 10\;m{\rm{/}}{{\rm{s}}^2}\))