Explanation:

The radius of curvature is given by
\({\rho = \frac{{m{v^3}}}{{|F \times v|}} = \frac{{m{v^3}}}{{Fv\sin \theta }} = \frac{{m{v^3}}}{{mgv\sin \theta }}}\)
\({(\therefore F = mg)}\)


\( \Rightarrow \quad \rho = \frac{{{v^2}}}{{g\sin \theta }}\)
\(\therefore \quad {\rho _{\min }} = \frac{{{v^2}}}{{g{{\left( {\sin \theta } \right)}_{\max }}}}\)
\(\therefore \quad {\rho _{{\rm{min }}}} = {v^2}/g\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\)
\(\left[ {{{(\sin \theta )}_{\max }} = 1} \right]{\rm{ }}\)
i.e. \(\theta=90^{\circ}\) is possible only when the projectile
is at maximum height.
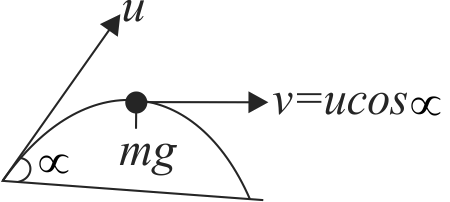
At the maximum height, velocity,
\(v = u\cos \propto \)
Given, \(\quad \propto \, = 60^\circ \) and \(u = 10\;m{s^{ - 1}}\)
\( = 10\cos 60^\circ = 5\;m{s^{ - 1}}\)
\(\therefore \quad {\rho _{\min }} = \frac{{5 \times 5}}{{9.8}} = 2.55\;m\)
[from Eqs.(1)]