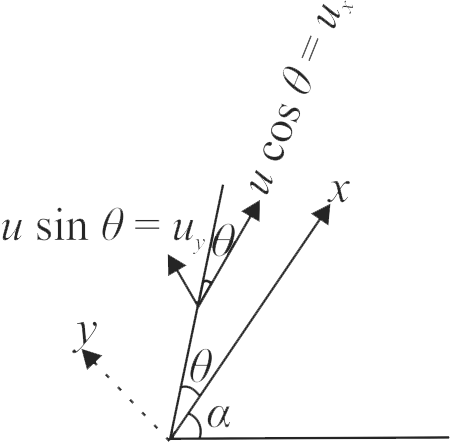362055
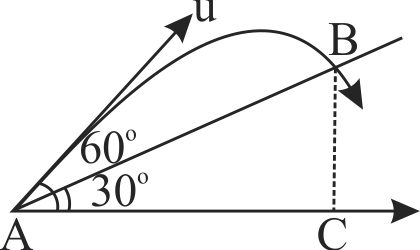
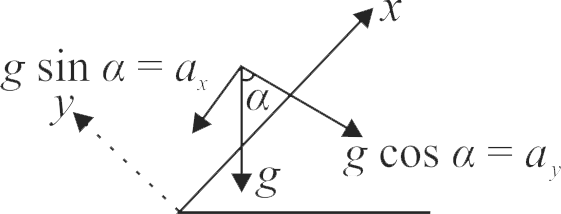
A plane is inclined at an angle \(\alpha=60^{\circ}\) w.r.t. horizontal. A particle is projected with a speed \(u = 6\;m{\rm{/}}s,\) from the base of the plane, making an angle \(\theta=10^{\circ}\) w.r.t. the plane. The distance from the base, at which particle hits the plane is
(Take \(g = 10\;m{\rm{/}}{s^2},\,\sin 10^\circ = 0.17,\,\cos 10^\circ = 0.98\))
362056
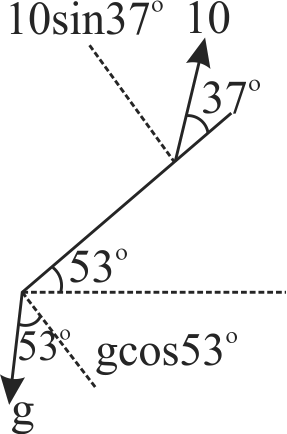
A particle is projected from the inclined plane at angle \(37^\circ \) with the inclined plane in upward direction with speed 10 \(m\)/\(s\). The angle of inclined plane with horizontal is \(53^\circ \). Then the maximum height attained by the particle from the inclined plane will be
362055
A plane is inclined at an angle \(\alpha=60^{\circ}\) w.r.t. horizontal. A particle is projected with a speed \(u = 6\;m{\rm{/}}s,\) from the base of the plane, making an angle \(\theta=10^{\circ}\) w.r.t. the plane. The distance from the base, at which particle hits the plane is
(Take \(g = 10\;m{\rm{/}}{s^2},\,\sin 10^\circ = 0.17,\,\cos 10^\circ = 0.98\))
362056
A particle is projected from the inclined plane at angle \(37^\circ \) with the inclined plane in upward direction with speed 10 \(m\)/\(s\). The angle of inclined plane with horizontal is \(53^\circ \). Then the maximum height attained by the particle from the inclined plane will be
362055
A plane is inclined at an angle \(\alpha=60^{\circ}\) w.r.t. horizontal. A particle is projected with a speed \(u = 6\;m{\rm{/}}s,\) from the base of the plane, making an angle \(\theta=10^{\circ}\) w.r.t. the plane. The distance from the base, at which particle hits the plane is
(Take \(g = 10\;m{\rm{/}}{s^2},\,\sin 10^\circ = 0.17,\,\cos 10^\circ = 0.98\))
362056
A particle is projected from the inclined plane at angle \(37^\circ \) with the inclined plane in upward direction with speed 10 \(m\)/\(s\). The angle of inclined plane with horizontal is \(53^\circ \). Then the maximum height attained by the particle from the inclined plane will be