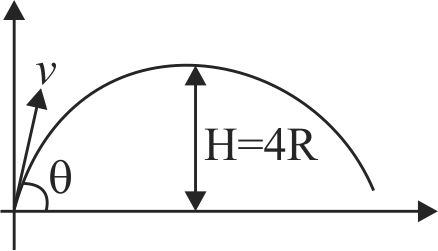
361965 A particle moving in a circle of radius \(R\) with a uniform speed takes a time \(T\) to complete one revolution. If this particle were projected with the same speed at an angle ‘ \(\theta \)’ to the horizontal, the maximum height attained by it equals 4\(R\) . The angle of projection \(\theta \), is then given by :
361965 A particle moving in a circle of radius \(R\) with a uniform speed takes a time \(T\) to complete one revolution. If this particle were projected with the same speed at an angle ‘ \(\theta \)’ to the horizontal, the maximum height attained by it equals 4\(R\) . The angle of projection \(\theta \), is then given by :
361965 A particle moving in a circle of radius \(R\) with a uniform speed takes a time \(T\) to complete one revolution. If this particle were projected with the same speed at an angle ‘ \(\theta \)’ to the horizontal, the maximum height attained by it equals 4\(R\) . The angle of projection \(\theta \), is then given by :
361965 A particle moving in a circle of radius \(R\) with a uniform speed takes a time \(T\) to complete one revolution. If this particle were projected with the same speed at an angle ‘ \(\theta \)’ to the horizontal, the maximum height attained by it equals 4\(R\) . The angle of projection \(\theta \), is then given by :