369711 The mean density of sea water is \(\rho\), and bulk modulus is \(B\). The change in density of sea water in going from the surface of water to a depth of \(h\) is

369712 A bottle has an opening of radius \(a\) and length b. A cork of length \(b\) and radius \((a+\Delta a)\) where \((a < < a)\) is compressed to fit into the opening
completely (see figure). If the bulk modulus of cork is B and frictional coefficient between the bottle and cork is then the force needed to

369713 In materials like aluminium and copper, the correct order of magnitude of various elastic modului is:

369714 A solid sphere of radius \(r\) made of a soft material of bulk modulus \(K\) is surrounded by a liquid in a cylindrical container. A massless piston of area a floats on the sueface of the liquid, convering entire cross section of cylindrical container. When a mass \(m\) is placed on the surface of the piston to compress the liquid, the dfractional decrement in the radius of the sphere, \(\left(\dfrac{d r}{r}\right)\), is:

369711 The mean density of sea water is \(\rho\), and bulk modulus is \(B\). The change in density of sea water in going from the surface of water to a depth of \(h\) is

369712 A bottle has an opening of radius \(a\) and length b. A cork of length \(b\) and radius \((a+\Delta a)\) where \((a < < a)\) is compressed to fit into the opening
completely (see figure). If the bulk modulus of cork is B and frictional coefficient between the bottle and cork is then the force needed to

369713 In materials like aluminium and copper, the correct order of magnitude of various elastic modului is:

369714 A solid sphere of radius \(r\) made of a soft material of bulk modulus \(K\) is surrounded by a liquid in a cylindrical container. A massless piston of area a floats on the sueface of the liquid, convering entire cross section of cylindrical container. When a mass \(m\) is placed on the surface of the piston to compress the liquid, the dfractional decrement in the radius of the sphere, \(\left(\dfrac{d r}{r}\right)\), is:

369711 The mean density of sea water is \(\rho\), and bulk modulus is \(B\). The change in density of sea water in going from the surface of water to a depth of \(h\) is

369712 A bottle has an opening of radius \(a\) and length b. A cork of length \(b\) and radius \((a+\Delta a)\) where \((a < < a)\) is compressed to fit into the opening
completely (see figure). If the bulk modulus of cork is B and frictional coefficient between the bottle and cork is then the force needed to

369713 In materials like aluminium and copper, the correct order of magnitude of various elastic modului is:

369714 A solid sphere of radius \(r\) made of a soft material of bulk modulus \(K\) is surrounded by a liquid in a cylindrical container. A massless piston of area a floats on the sueface of the liquid, convering entire cross section of cylindrical container. When a mass \(m\) is placed on the surface of the piston to compress the liquid, the dfractional decrement in the radius of the sphere, \(\left(\dfrac{d r}{r}\right)\), is:

369711 The mean density of sea water is \(\rho\), and bulk modulus is \(B\). The change in density of sea water in going from the surface of water to a depth of \(h\) is

369712 A bottle has an opening of radius \(a\) and length b. A cork of length \(b\) and radius \((a+\Delta a)\) where \((a < < a)\) is compressed to fit into the opening
completely (see figure). If the bulk modulus of cork is B and frictional coefficient between the bottle and cork is then the force needed to

369713 In materials like aluminium and copper, the correct order of magnitude of various elastic modului is:

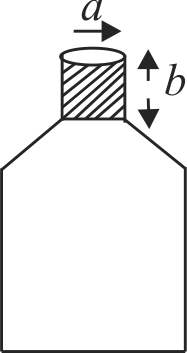
369714 A solid sphere of radius \(r\) made of a soft material of bulk modulus \(K\) is surrounded by a liquid in a cylindrical container. A massless piston of area a floats on the sueface of the liquid, convering entire cross section of cylindrical container. When a mass \(m\) is placed on the surface of the piston to compress the liquid, the dfractional decrement in the radius of the sphere, \(\left(\dfrac{d r}{r}\right)\), is: