369810 A student performs an experiment to determine the Young's modulus of a wire, exactly \(2 m\) long, by searle's method. The student measures the extension in the length of the wire to be \(0.8\;mm\) with an uncertainty of \( \pm 0.05\;mm\) at a load of exactly \(1.0\;kg\). The student also,measures the diameter of the wire to be \(0.4\;mm\) with an uncertainty \( \pm 0.01\;mm.\,{\text{Take}}\,g = 9.8\;m/{s^2}\) (exact). The Young's modulus obtained from the reading is
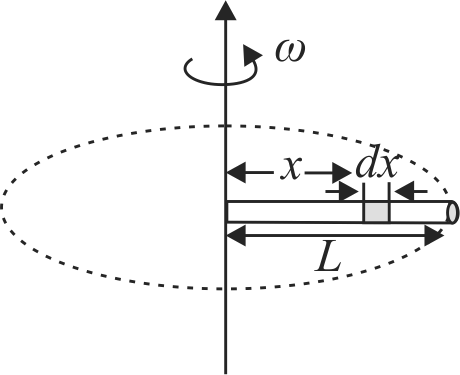
369812 A uniform rod of mass \(m\), length \(L\), area of crosssection A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity \(\omega\) in a horizontal plane. If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
369810 A student performs an experiment to determine the Young's modulus of a wire, exactly \(2 m\) long, by searle's method. The student measures the extension in the length of the wire to be \(0.8\;mm\) with an uncertainty of \( \pm 0.05\;mm\) at a load of exactly \(1.0\;kg\). The student also,measures the diameter of the wire to be \(0.4\;mm\) with an uncertainty \( \pm 0.01\;mm.\,{\text{Take}}\,g = 9.8\;m/{s^2}\) (exact). The Young's modulus obtained from the reading is
369812 A uniform rod of mass \(m\), length \(L\), area of crosssection A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity \(\omega\) in a horizontal plane. If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
369810 A student performs an experiment to determine the Young's modulus of a wire, exactly \(2 m\) long, by searle's method. The student measures the extension in the length of the wire to be \(0.8\;mm\) with an uncertainty of \( \pm 0.05\;mm\) at a load of exactly \(1.0\;kg\). The student also,measures the diameter of the wire to be \(0.4\;mm\) with an uncertainty \( \pm 0.01\;mm.\,{\text{Take}}\,g = 9.8\;m/{s^2}\) (exact). The Young's modulus obtained from the reading is
369812 A uniform rod of mass \(m\), length \(L\), area of crosssection A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity \(\omega\) in a horizontal plane. If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
369810 A student performs an experiment to determine the Young's modulus of a wire, exactly \(2 m\) long, by searle's method. The student measures the extension in the length of the wire to be \(0.8\;mm\) with an uncertainty of \( \pm 0.05\;mm\) at a load of exactly \(1.0\;kg\). The student also,measures the diameter of the wire to be \(0.4\;mm\) with an uncertainty \( \pm 0.01\;mm.\,{\text{Take}}\,g = 9.8\;m/{s^2}\) (exact). The Young's modulus obtained from the reading is
369812 A uniform rod of mass \(m\), length \(L\), area of crosssection A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity \(\omega\) in a horizontal plane. If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is