361356
In the figure shown, a thin disc of radius \(R\) is is located on the surface of an oil filled container. The distance between the disc and the lower base of the container is \(D\). The disc is driven at constant angular speed \(\omega\) about the axis passing through the centre of the disc. The viscosity of the oil is \(\eta\). Find the torque required to drive the disc.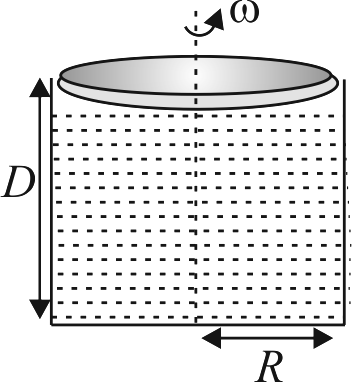
361357
A cubical block of side ' \(a\) ' and density ' \(\rho\) ' slides over a fixed inclined plane with constant velocity ' \(v\) '. There is a thin film of viscous fluid of thickness ' \(t\) ' between the plane and the block. Then the coefficient of viscosity of the thin film will be: (Acceleration due to gravity is \(g\) )
361359 The radius of a pipe carrying a liquid decreases by \(20 \%\) because of deposits on the inner surface. By how many times would the pressure difference between the ends of the constricted pipe should be increased to original pressure difference to maintain a constant flow rate?
361356
In the figure shown, a thin disc of radius \(R\) is is located on the surface of an oil filled container. The distance between the disc and the lower base of the container is \(D\). The disc is driven at constant angular speed \(\omega\) about the axis passing through the centre of the disc. The viscosity of the oil is \(\eta\). Find the torque required to drive the disc.
361357
A cubical block of side ' \(a\) ' and density ' \(\rho\) ' slides over a fixed inclined plane with constant velocity ' \(v\) '. There is a thin film of viscous fluid of thickness ' \(t\) ' between the plane and the block. Then the coefficient of viscosity of the thin film will be: (Acceleration due to gravity is \(g\) )
361359 The radius of a pipe carrying a liquid decreases by \(20 \%\) because of deposits on the inner surface. By how many times would the pressure difference between the ends of the constricted pipe should be increased to original pressure difference to maintain a constant flow rate?
361356
In the figure shown, a thin disc of radius \(R\) is is located on the surface of an oil filled container. The distance between the disc and the lower base of the container is \(D\). The disc is driven at constant angular speed \(\omega\) about the axis passing through the centre of the disc. The viscosity of the oil is \(\eta\). Find the torque required to drive the disc.
361357
A cubical block of side ' \(a\) ' and density ' \(\rho\) ' slides over a fixed inclined plane with constant velocity ' \(v\) '. There is a thin film of viscous fluid of thickness ' \(t\) ' between the plane and the block. Then the coefficient of viscosity of the thin film will be: (Acceleration due to gravity is \(g\) )
361359 The radius of a pipe carrying a liquid decreases by \(20 \%\) because of deposits on the inner surface. By how many times would the pressure difference between the ends of the constricted pipe should be increased to original pressure difference to maintain a constant flow rate?
361356
In the figure shown, a thin disc of radius \(R\) is is located on the surface of an oil filled container. The distance between the disc and the lower base of the container is \(D\). The disc is driven at constant angular speed \(\omega\) about the axis passing through the centre of the disc. The viscosity of the oil is \(\eta\). Find the torque required to drive the disc.
361357
A cubical block of side ' \(a\) ' and density ' \(\rho\) ' slides over a fixed inclined plane with constant velocity ' \(v\) '. There is a thin film of viscous fluid of thickness ' \(t\) ' between the plane and the block. Then the coefficient of viscosity of the thin film will be: (Acceleration due to gravity is \(g\) )
361359 The radius of a pipe carrying a liquid decreases by \(20 \%\) because of deposits on the inner surface. By how many times would the pressure difference between the ends of the constricted pipe should be increased to original pressure difference to maintain a constant flow rate?
361356
In the figure shown, a thin disc of radius \(R\) is is located on the surface of an oil filled container. The distance between the disc and the lower base of the container is \(D\). The disc is driven at constant angular speed \(\omega\) about the axis passing through the centre of the disc. The viscosity of the oil is \(\eta\). Find the torque required to drive the disc.
361357
A cubical block of side ' \(a\) ' and density ' \(\rho\) ' slides over a fixed inclined plane with constant velocity ' \(v\) '. There is a thin film of viscous fluid of thickness ' \(t\) ' between the plane and the block. Then the coefficient of viscosity of the thin film will be: (Acceleration due to gravity is \(g\) )
361359 The radius of a pipe carrying a liquid decreases by \(20 \%\) because of deposits on the inner surface. By how many times would the pressure difference between the ends of the constricted pipe should be increased to original pressure difference to maintain a constant flow rate?
