361346
A fluid with viscosity \(\eta\) fills the space between two along co-axial cylinders of radii \(R_{1}\) and \(R_{2}\). The inner cylinder is stationary while the outer one is rotated with a constant angular velocity \(\omega_{2}\). The fluid flow is laminar. Taking into account that the friction force acting on a unit area of cylindrical surface radius \(r\) is defined by the formula \(\sigma=\eta r\left(\dfrac{d \omega}{d r}\right)\), find the angular velocity of rotating fluid as a function of radius \(r\).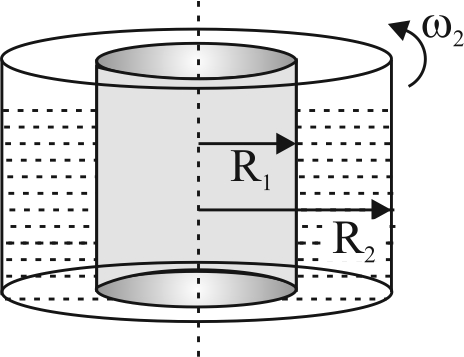
361346
A fluid with viscosity \(\eta\) fills the space between two along co-axial cylinders of radii \(R_{1}\) and \(R_{2}\). The inner cylinder is stationary while the outer one is rotated with a constant angular velocity \(\omega_{2}\). The fluid flow is laminar. Taking into account that the friction force acting on a unit area of cylindrical surface radius \(r\) is defined by the formula \(\sigma=\eta r\left(\dfrac{d \omega}{d r}\right)\), find the angular velocity of rotating fluid as a function of radius \(r\).
361346
A fluid with viscosity \(\eta\) fills the space between two along co-axial cylinders of radii \(R_{1}\) and \(R_{2}\). The inner cylinder is stationary while the outer one is rotated with a constant angular velocity \(\omega_{2}\). The fluid flow is laminar. Taking into account that the friction force acting on a unit area of cylindrical surface radius \(r\) is defined by the formula \(\sigma=\eta r\left(\dfrac{d \omega}{d r}\right)\), find the angular velocity of rotating fluid as a function of radius \(r\).
361346
A fluid with viscosity \(\eta\) fills the space between two along co-axial cylinders of radii \(R_{1}\) and \(R_{2}\). The inner cylinder is stationary while the outer one is rotated with a constant angular velocity \(\omega_{2}\). The fluid flow is laminar. Taking into account that the friction force acting on a unit area of cylindrical surface radius \(r\) is defined by the formula \(\sigma=\eta r\left(\dfrac{d \omega}{d r}\right)\), find the angular velocity of rotating fluid as a function of radius \(r\).
