361316
A ring is cut from a platinum tube of \(8.5\;\,cm\) internal and \(8.7\;cm\) external diameter. It is supported horizontally from a balance so that it comes in contact with the water in a glass vessel. What is the surface tension of water if an extra \(3.97\;\,g\) weight is required to pull it away from water ? \(\left( {g = 980\;cm/{s^2}} \right)\)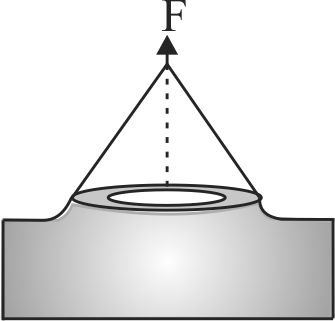
361316
A ring is cut from a platinum tube of \(8.5\;\,cm\) internal and \(8.7\;cm\) external diameter. It is supported horizontally from a balance so that it comes in contact with the water in a glass vessel. What is the surface tension of water if an extra \(3.97\;\,g\) weight is required to pull it away from water ? \(\left( {g = 980\;cm/{s^2}} \right)\)
361316
A ring is cut from a platinum tube of \(8.5\;\,cm\) internal and \(8.7\;cm\) external diameter. It is supported horizontally from a balance so that it comes in contact with the water in a glass vessel. What is the surface tension of water if an extra \(3.97\;\,g\) weight is required to pull it away from water ? \(\left( {g = 980\;cm/{s^2}} \right)\)
361316
A ring is cut from a platinum tube of \(8.5\;\,cm\) internal and \(8.7\;cm\) external diameter. It is supported horizontally from a balance so that it comes in contact with the water in a glass vessel. What is the surface tension of water if an extra \(3.97\;\,g\) weight is required to pull it away from water ? \(\left( {g = 980\;cm/{s^2}} \right)\)
361316
A ring is cut from a platinum tube of \(8.5\;\,cm\) internal and \(8.7\;cm\) external diameter. It is supported horizontally from a balance so that it comes in contact with the water in a glass vessel. What is the surface tension of water if an extra \(3.97\;\,g\) weight is required to pull it away from water ? \(\left( {g = 980\;cm/{s^2}} \right)\)