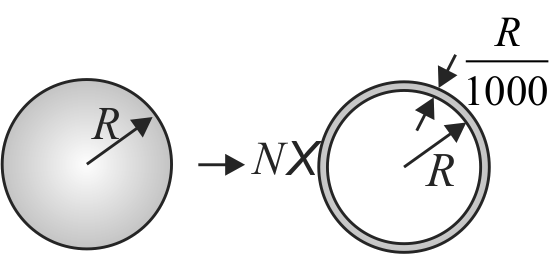361275
Consider a liquid drop of radius \(R\) and density \(\rho\). Now the drop is blown into \((N)\) large number of bubbles each having radius \(R\) and surface thickness \(\dfrac{R}{1000}\). If \(T\) is the surface tension of the liquid find the work done by the external agent to blow the bubbles.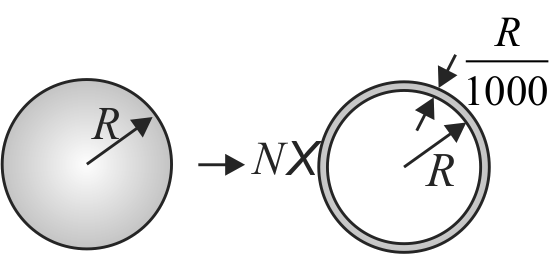
361275
Consider a liquid drop of radius \(R\) and density \(\rho\). Now the drop is blown into \((N)\) large number of bubbles each having radius \(R\) and surface thickness \(\dfrac{R}{1000}\). If \(T\) is the surface tension of the liquid find the work done by the external agent to blow the bubbles.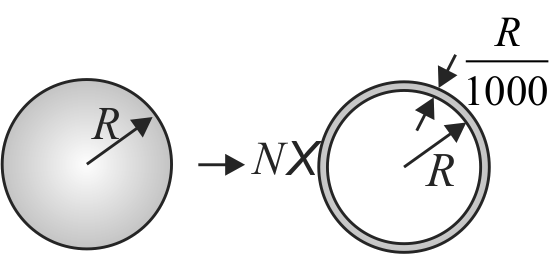
361275
Consider a liquid drop of radius \(R\) and density \(\rho\). Now the drop is blown into \((N)\) large number of bubbles each having radius \(R\) and surface thickness \(\dfrac{R}{1000}\). If \(T\) is the surface tension of the liquid find the work done by the external agent to blow the bubbles.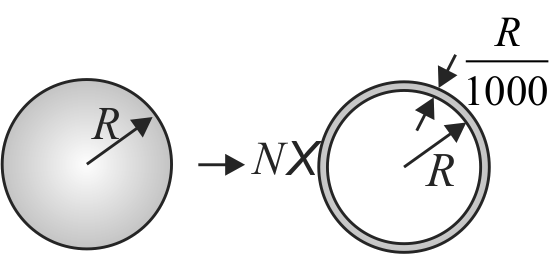
361275
Consider a liquid drop of radius \(R\) and density \(\rho\). Now the drop is blown into \((N)\) large number of bubbles each having radius \(R\) and surface thickness \(\dfrac{R}{1000}\). If \(T\) is the surface tension of the liquid find the work done by the external agent to blow the bubbles.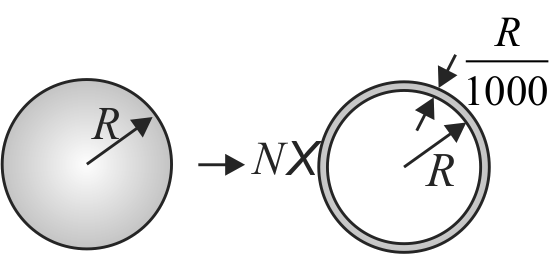
361275
Consider a liquid drop of radius \(R\) and density \(\rho\). Now the drop is blown into \((N)\) large number of bubbles each having radius \(R\) and surface thickness \(\dfrac{R}{1000}\). If \(T\) is the surface tension of the liquid find the work done by the external agent to blow the bubbles.