361237 If excess of pressure inside a soap bubble of radius \(2\;cm\) is balanced by that due to column of oil of (specific gravity \( = 0.8)2\;mm\) high. What is the surface tension of soap bubble?

361238 The rain drops are in spherical shape due to

361239 A soap bubble has radius \(r\). The work done in increasing its radius to three times its original radius, without any rise of temperature, is (Given: surface tension of soap solution is \(T\))

361240 Calculate the pressure inside a small air bubble of radius \(0.01\;mm\) situated at a depth of \(h = 20\;m\) below the free surface of liquid of density \({\rho _1} = {10^3}\;kg/{m^3},{\rho _2} = 8000\;kg/{m^3}\) and surface tension \({T_2} = 7.5 \times {10^{ - 2}}\;N/m\). The thickness of the first liquid is \({h_1} = 15\;m\,{\rm{and}}\,{h_2} = 25\;m\).

361237 If excess of pressure inside a soap bubble of radius \(2\;cm\) is balanced by that due to column of oil of (specific gravity \( = 0.8)2\;mm\) high. What is the surface tension of soap bubble?

361238 The rain drops are in spherical shape due to

361239 A soap bubble has radius \(r\). The work done in increasing its radius to three times its original radius, without any rise of temperature, is (Given: surface tension of soap solution is \(T\))

361240 Calculate the pressure inside a small air bubble of radius \(0.01\;mm\) situated at a depth of \(h = 20\;m\) below the free surface of liquid of density \({\rho _1} = {10^3}\;kg/{m^3},{\rho _2} = 8000\;kg/{m^3}\) and surface tension \({T_2} = 7.5 \times {10^{ - 2}}\;N/m\). The thickness of the first liquid is \({h_1} = 15\;m\,{\rm{and}}\,{h_2} = 25\;m\).

361237 If excess of pressure inside a soap bubble of radius \(2\;cm\) is balanced by that due to column of oil of (specific gravity \( = 0.8)2\;mm\) high. What is the surface tension of soap bubble?

361238 The rain drops are in spherical shape due to

361239 A soap bubble has radius \(r\). The work done in increasing its radius to three times its original radius, without any rise of temperature, is (Given: surface tension of soap solution is \(T\))

361240 Calculate the pressure inside a small air bubble of radius \(0.01\;mm\) situated at a depth of \(h = 20\;m\) below the free surface of liquid of density \({\rho _1} = {10^3}\;kg/{m^3},{\rho _2} = 8000\;kg/{m^3}\) and surface tension \({T_2} = 7.5 \times {10^{ - 2}}\;N/m\). The thickness of the first liquid is \({h_1} = 15\;m\,{\rm{and}}\,{h_2} = 25\;m\).

361237 If excess of pressure inside a soap bubble of radius \(2\;cm\) is balanced by that due to column of oil of (specific gravity \( = 0.8)2\;mm\) high. What is the surface tension of soap bubble?

361238 The rain drops are in spherical shape due to

361239 A soap bubble has radius \(r\). The work done in increasing its radius to three times its original radius, without any rise of temperature, is (Given: surface tension of soap solution is \(T\))

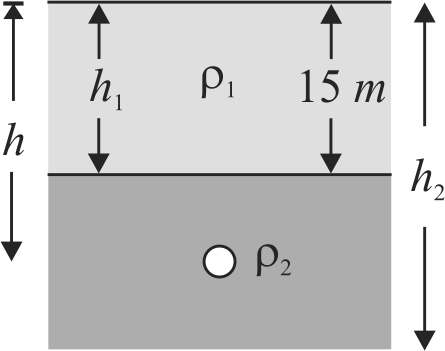
361240 Calculate the pressure inside a small air bubble of radius \(0.01\;mm\) situated at a depth of \(h = 20\;m\) below the free surface of liquid of density \({\rho _1} = {10^3}\;kg/{m^3},{\rho _2} = 8000\;kg/{m^3}\) and surface tension \({T_2} = 7.5 \times {10^{ - 2}}\;N/m\). The thickness of the first liquid is \({h_1} = 15\;m\,{\rm{and}}\,{h_2} = 25\;m\).