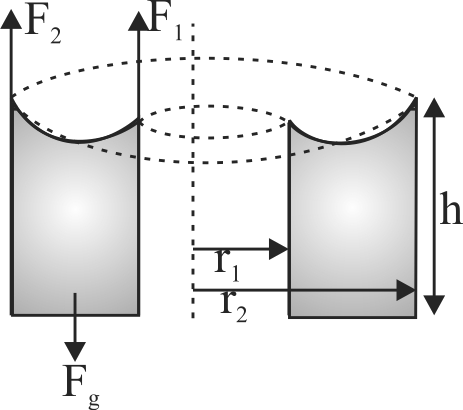
361190 Two narrow tube of diameters ' \(d_{1}\) ' and ' \(d_{2}\) ' are joined together to form a \(U\) tube open at both ends. If \(U\) tube contains water, the difference in water levels in the limbs is ( \(T\) is the surface tension of water, angle of contact \(=\) zero and density of water \(=\rho, g=\) acceleration due to gravity)
361192
A glass rod of radius \(r_{1}\) is inserted symmetrically into a vertical capillary tube of radius \(r_{2}\) such that their lower ends are at the same level. The arrangement is now dipped in water. The height to which water will rise into the tube will be ( \(s=\) surface tension of water, \(\rho=\) density of water)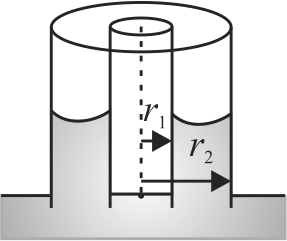
361193
It two glass plates have water between them and are separated by very small distance (see figure), it is very diffucult to pull them apart. It is because the water in between forms cylindrical surface on the side that gives rise to lower pressure in the water in comparison to atmosphere. If the radius of the cylindrical surface is \(R\) and surface tension of water is \(T\) then the pressure in water between the plates is lower by :
361190 Two narrow tube of diameters ' \(d_{1}\) ' and ' \(d_{2}\) ' are joined together to form a \(U\) tube open at both ends. If \(U\) tube contains water, the difference in water levels in the limbs is ( \(T\) is the surface tension of water, angle of contact \(=\) zero and density of water \(=\rho, g=\) acceleration due to gravity)
361192
A glass rod of radius \(r_{1}\) is inserted symmetrically into a vertical capillary tube of radius \(r_{2}\) such that their lower ends are at the same level. The arrangement is now dipped in water. The height to which water will rise into the tube will be ( \(s=\) surface tension of water, \(\rho=\) density of water)
361193
It two glass plates have water between them and are separated by very small distance (see figure), it is very diffucult to pull them apart. It is because the water in between forms cylindrical surface on the side that gives rise to lower pressure in the water in comparison to atmosphere. If the radius of the cylindrical surface is \(R\) and surface tension of water is \(T\) then the pressure in water between the plates is lower by :
361190 Two narrow tube of diameters ' \(d_{1}\) ' and ' \(d_{2}\) ' are joined together to form a \(U\) tube open at both ends. If \(U\) tube contains water, the difference in water levels in the limbs is ( \(T\) is the surface tension of water, angle of contact \(=\) zero and density of water \(=\rho, g=\) acceleration due to gravity)
361192
A glass rod of radius \(r_{1}\) is inserted symmetrically into a vertical capillary tube of radius \(r_{2}\) such that their lower ends are at the same level. The arrangement is now dipped in water. The height to which water will rise into the tube will be ( \(s=\) surface tension of water, \(\rho=\) density of water)
361193
It two glass plates have water between them and are separated by very small distance (see figure), it is very diffucult to pull them apart. It is because the water in between forms cylindrical surface on the side that gives rise to lower pressure in the water in comparison to atmosphere. If the radius of the cylindrical surface is \(R\) and surface tension of water is \(T\) then the pressure in water between the plates is lower by :
361190 Two narrow tube of diameters ' \(d_{1}\) ' and ' \(d_{2}\) ' are joined together to form a \(U\) tube open at both ends. If \(U\) tube contains water, the difference in water levels in the limbs is ( \(T\) is the surface tension of water, angle of contact \(=\) zero and density of water \(=\rho, g=\) acceleration due to gravity)
361192
A glass rod of radius \(r_{1}\) is inserted symmetrically into a vertical capillary tube of radius \(r_{2}\) such that their lower ends are at the same level. The arrangement is now dipped in water. The height to which water will rise into the tube will be ( \(s=\) surface tension of water, \(\rho=\) density of water)
361193
It two glass plates have water between them and are separated by very small distance (see figure), it is very diffucult to pull them apart. It is because the water in between forms cylindrical surface on the side that gives rise to lower pressure in the water in comparison to atmosphere. If the radius of the cylindrical surface is \(R\) and surface tension of water is \(T\) then the pressure in water between the plates is lower by :