360913
Figure shows a liquid being pushed out of a tube by pressing a piston. The cross-sectional area of the piston is \(1\;c{m^2}\) and that of the tube at the outlet is \(20\;m{m^2}\). If the piston is pushed at a speed of \(1\,cm{s^{ - 1}}\), then the velocity of the outgoing liquid is :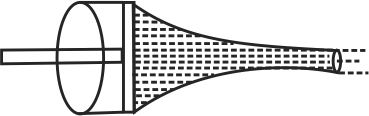
360915 Water is flowing through two horizontal pipes of different diameters which are connected together. The diameters of the two pipes are 3 \(cm\) and 6 \(cm\) respectively. If the speed of water in narrow pipe is \(4\;m/\sec \) and the pressure is \(2.0 \times 10^{4}\) pascal, then the speed of water in the wider pipe is :-
360917
Consider a water jar of radius \(R\) that has water filled up to height \(H\) and is kept on a stand of height \(h\) (see figure). Through a hole of radius \(r\) \((r < < R)\) at its bottom, the water leaks out and the stream of water coming down towards the ground has a shape like a funnel as shown in the figure. If the radius of the cross-section of water stream when it hits the ground is \(x\). Then: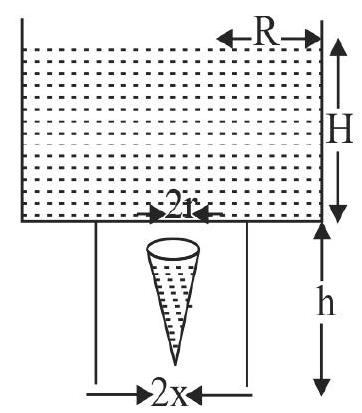
360913
Figure shows a liquid being pushed out of a tube by pressing a piston. The cross-sectional area of the piston is \(1\;c{m^2}\) and that of the tube at the outlet is \(20\;m{m^2}\). If the piston is pushed at a speed of \(1\,cm{s^{ - 1}}\), then the velocity of the outgoing liquid is :
360915 Water is flowing through two horizontal pipes of different diameters which are connected together. The diameters of the two pipes are 3 \(cm\) and 6 \(cm\) respectively. If the speed of water in narrow pipe is \(4\;m/\sec \) and the pressure is \(2.0 \times 10^{4}\) pascal, then the speed of water in the wider pipe is :-
360917
Consider a water jar of radius \(R\) that has water filled up to height \(H\) and is kept on a stand of height \(h\) (see figure). Through a hole of radius \(r\) \((r < < R)\) at its bottom, the water leaks out and the stream of water coming down towards the ground has a shape like a funnel as shown in the figure. If the radius of the cross-section of water stream when it hits the ground is \(x\). Then:
360913
Figure shows a liquid being pushed out of a tube by pressing a piston. The cross-sectional area of the piston is \(1\;c{m^2}\) and that of the tube at the outlet is \(20\;m{m^2}\). If the piston is pushed at a speed of \(1\,cm{s^{ - 1}}\), then the velocity of the outgoing liquid is :
360915 Water is flowing through two horizontal pipes of different diameters which are connected together. The diameters of the two pipes are 3 \(cm\) and 6 \(cm\) respectively. If the speed of water in narrow pipe is \(4\;m/\sec \) and the pressure is \(2.0 \times 10^{4}\) pascal, then the speed of water in the wider pipe is :-
360917
Consider a water jar of radius \(R\) that has water filled up to height \(H\) and is kept on a stand of height \(h\) (see figure). Through a hole of radius \(r\) \((r < < R)\) at its bottom, the water leaks out and the stream of water coming down towards the ground has a shape like a funnel as shown in the figure. If the radius of the cross-section of water stream when it hits the ground is \(x\). Then:
360913
Figure shows a liquid being pushed out of a tube by pressing a piston. The cross-sectional area of the piston is \(1\;c{m^2}\) and that of the tube at the outlet is \(20\;m{m^2}\). If the piston is pushed at a speed of \(1\,cm{s^{ - 1}}\), then the velocity of the outgoing liquid is :
360915 Water is flowing through two horizontal pipes of different diameters which are connected together. The diameters of the two pipes are 3 \(cm\) and 6 \(cm\) respectively. If the speed of water in narrow pipe is \(4\;m/\sec \) and the pressure is \(2.0 \times 10^{4}\) pascal, then the speed of water in the wider pipe is :-
360917
Consider a water jar of radius \(R\) that has water filled up to height \(H\) and is kept on a stand of height \(h\) (see figure). Through a hole of radius \(r\) \((r < < R)\) at its bottom, the water leaks out and the stream of water coming down towards the ground has a shape like a funnel as shown in the figure. If the radius of the cross-section of water stream when it hits the ground is \(x\). Then:
360913
Figure shows a liquid being pushed out of a tube by pressing a piston. The cross-sectional area of the piston is \(1\;c{m^2}\) and that of the tube at the outlet is \(20\;m{m^2}\). If the piston is pushed at a speed of \(1\,cm{s^{ - 1}}\), then the velocity of the outgoing liquid is :
360915 Water is flowing through two horizontal pipes of different diameters which are connected together. The diameters of the two pipes are 3 \(cm\) and 6 \(cm\) respectively. If the speed of water in narrow pipe is \(4\;m/\sec \) and the pressure is \(2.0 \times 10^{4}\) pascal, then the speed of water in the wider pipe is :-
360917
Consider a water jar of radius \(R\) that has water filled up to height \(H\) and is kept on a stand of height \(h\) (see figure). Through a hole of radius \(r\) \((r < < R)\) at its bottom, the water leaks out and the stream of water coming down towards the ground has a shape like a funnel as shown in the figure. If the radius of the cross-section of water stream when it hits the ground is \(x\). Then:
