360895 A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section \(A_{1}\) and \(A_{2}\), are \(v_{1}\) and \(v_{2}\), respectively. The difference in the levels of the liquid in the two vertical tubes is \(h\). Then

360896 The cylindrical tube of a spray pump has a cross-section of \(8\;c{m^2}\), one end of which has 40 fine holes each of area \({10^{ - 8}}\;{m^2}\). If the liquid flows inside the tube with a speed of \(0.15\;m{s^{ - 1}}\), the speed with which the liquid is ejected through the holes is

360897 A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of crosssection \({A_1}\) and \({A_2}\), are \({v_1}\) and \({v_2}\), respectively. The difference in the levels of the liquid in the two vertical tubes is \(3\;h.\) If \({A_2}\) is one by four times \({A_1},v_2^2 = khg.\) Find value of \(k.\)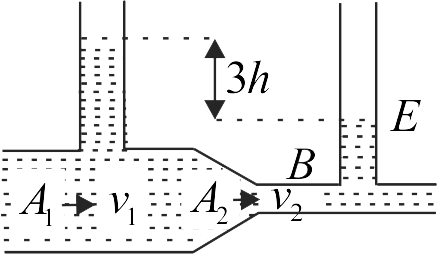

360898 Read the Statement - A and Statement - B carefully to mark the correct options given below.
Statement A :
When speed of liquid is zero everywhere, pressure difference at any two points depends on equation
\(P_{1}-P_{2}=\rho g\left(h_{2}-h_{1}\right)\).
Statement B :
In venturi tube shown \(2 g h=v_{1}^{2}-v_{2}^{2}\)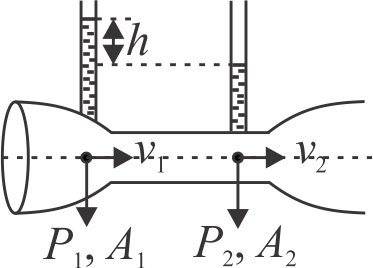

360895 A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section \(A_{1}\) and \(A_{2}\), are \(v_{1}\) and \(v_{2}\), respectively. The difference in the levels of the liquid in the two vertical tubes is \(h\). Then

360896 The cylindrical tube of a spray pump has a cross-section of \(8\;c{m^2}\), one end of which has 40 fine holes each of area \({10^{ - 8}}\;{m^2}\). If the liquid flows inside the tube with a speed of \(0.15\;m{s^{ - 1}}\), the speed with which the liquid is ejected through the holes is

360897 A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of crosssection \({A_1}\) and \({A_2}\), are \({v_1}\) and \({v_2}\), respectively. The difference in the levels of the liquid in the two vertical tubes is \(3\;h.\) If \({A_2}\) is one by four times \({A_1},v_2^2 = khg.\) Find value of \(k.\)

360898 Read the Statement - A and Statement - B carefully to mark the correct options given below.
Statement A :
When speed of liquid is zero everywhere, pressure difference at any two points depends on equation
\(P_{1}-P_{2}=\rho g\left(h_{2}-h_{1}\right)\).
Statement B :
In venturi tube shown \(2 g h=v_{1}^{2}-v_{2}^{2}\)

360895 A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section \(A_{1}\) and \(A_{2}\), are \(v_{1}\) and \(v_{2}\), respectively. The difference in the levels of the liquid in the two vertical tubes is \(h\). Then

360896 The cylindrical tube of a spray pump has a cross-section of \(8\;c{m^2}\), one end of which has 40 fine holes each of area \({10^{ - 8}}\;{m^2}\). If the liquid flows inside the tube with a speed of \(0.15\;m{s^{ - 1}}\), the speed with which the liquid is ejected through the holes is

360897 A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of crosssection \({A_1}\) and \({A_2}\), are \({v_1}\) and \({v_2}\), respectively. The difference in the levels of the liquid in the two vertical tubes is \(3\;h.\) If \({A_2}\) is one by four times \({A_1},v_2^2 = khg.\) Find value of \(k.\)

360898 Read the Statement - A and Statement - B carefully to mark the correct options given below.
Statement A :
When speed of liquid is zero everywhere, pressure difference at any two points depends on equation
\(P_{1}-P_{2}=\rho g\left(h_{2}-h_{1}\right)\).
Statement B :
In venturi tube shown \(2 g h=v_{1}^{2}-v_{2}^{2}\)

360895 A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section \(A_{1}\) and \(A_{2}\), are \(v_{1}\) and \(v_{2}\), respectively. The difference in the levels of the liquid in the two vertical tubes is \(h\). Then

360896 The cylindrical tube of a spray pump has a cross-section of \(8\;c{m^2}\), one end of which has 40 fine holes each of area \({10^{ - 8}}\;{m^2}\). If the liquid flows inside the tube with a speed of \(0.15\;m{s^{ - 1}}\), the speed with which the liquid is ejected through the holes is

360897 A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of crosssection \({A_1}\) and \({A_2}\), are \({v_1}\) and \({v_2}\), respectively. The difference in the levels of the liquid in the two vertical tubes is \(3\;h.\) If \({A_2}\) is one by four times \({A_1},v_2^2 = khg.\) Find value of \(k.\)

360898 Read the Statement - A and Statement - B carefully to mark the correct options given below.
Statement A :
When speed of liquid is zero everywhere, pressure difference at any two points depends on equation
\(P_{1}-P_{2}=\rho g\left(h_{2}-h_{1}\right)\).
Statement B :
In venturi tube shown \(2 g h=v_{1}^{2}-v_{2}^{2}\)