Explanation:
The new magnetic moment is given as follows
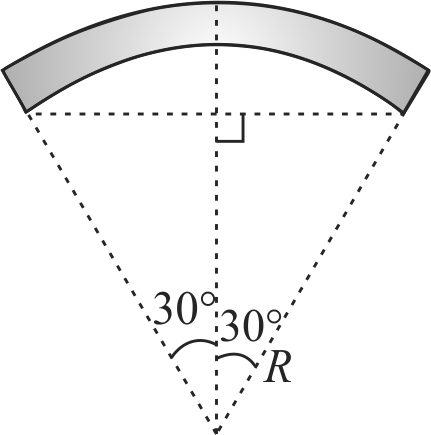
\(M = {M_1} = \left( {R \times \frac{\pi }{3}} \right)m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
\({M_2} = \left( {2\,R\,\sin \,30^\circ } \right)m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
From equations (1) and (2)
\(\frac{M}{{{M_2}}} = \frac{\pi }{3} \Rightarrow {M_2} = \frac{{3M}}{\pi }\)
% change in magnetic moment
\( = \frac{{{M_2} - {M_1}}}{{{M_1}}} \times 100 = \left( {\frac{{\frac{{3M}}{\pi } - M}}{M}} \right) \times 100\)
\( = - 4 \cdot 5\% \).
So \(4 \cdot 5\% \) decreases.