360566 A circular loop of radius \(0.3\;cm\) lies parallel to a much bigger circular loop of radius \(20\;cm\). The centre of the smaller loop is on the axis of the bigger loop. The distance between their centres is \(15\;cm\). If a current of \(2.0\;A\) flows through the smaller loop, then the flux linked with bigger loop
360567
A uniform magnetic field of strength \({B=2 m T}\) exists vertically downwards. These magnetic field lines pass through a closed surface as shown in the figure. The closed surface consists of a hemisphere \({S_{1}}\), a right circular cone \({S_{2}}\) and a circular surface \({S_{3}}\). The magnetic flux through \({S_{1}}\) and \({S_{2}}\) are respectively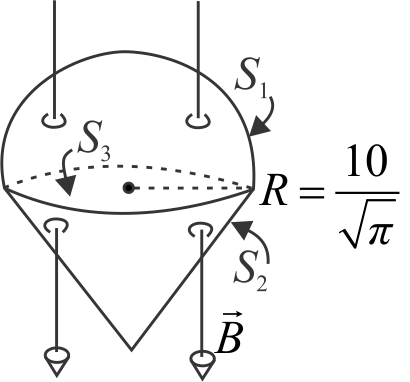
360566 A circular loop of radius \(0.3\;cm\) lies parallel to a much bigger circular loop of radius \(20\;cm\). The centre of the smaller loop is on the axis of the bigger loop. The distance between their centres is \(15\;cm\). If a current of \(2.0\;A\) flows through the smaller loop, then the flux linked with bigger loop
360567
A uniform magnetic field of strength \({B=2 m T}\) exists vertically downwards. These magnetic field lines pass through a closed surface as shown in the figure. The closed surface consists of a hemisphere \({S_{1}}\), a right circular cone \({S_{2}}\) and a circular surface \({S_{3}}\). The magnetic flux through \({S_{1}}\) and \({S_{2}}\) are respectively
360566 A circular loop of radius \(0.3\;cm\) lies parallel to a much bigger circular loop of radius \(20\;cm\). The centre of the smaller loop is on the axis of the bigger loop. The distance between their centres is \(15\;cm\). If a current of \(2.0\;A\) flows through the smaller loop, then the flux linked with bigger loop
360567
A uniform magnetic field of strength \({B=2 m T}\) exists vertically downwards. These magnetic field lines pass through a closed surface as shown in the figure. The closed surface consists of a hemisphere \({S_{1}}\), a right circular cone \({S_{2}}\) and a circular surface \({S_{3}}\). The magnetic flux through \({S_{1}}\) and \({S_{2}}\) are respectively
360566 A circular loop of radius \(0.3\;cm\) lies parallel to a much bigger circular loop of radius \(20\;cm\). The centre of the smaller loop is on the axis of the bigger loop. The distance between their centres is \(15\;cm\). If a current of \(2.0\;A\) flows through the smaller loop, then the flux linked with bigger loop
360567
A uniform magnetic field of strength \({B=2 m T}\) exists vertically downwards. These magnetic field lines pass through a closed surface as shown in the figure. The closed surface consists of a hemisphere \({S_{1}}\), a right circular cone \({S_{2}}\) and a circular surface \({S_{3}}\). The magnetic flux through \({S_{1}}\) and \({S_{2}}\) are respectively
360566 A circular loop of radius \(0.3\;cm\) lies parallel to a much bigger circular loop of radius \(20\;cm\). The centre of the smaller loop is on the axis of the bigger loop. The distance between their centres is \(15\;cm\). If a current of \(2.0\;A\) flows through the smaller loop, then the flux linked with bigger loop
360567
A uniform magnetic field of strength \({B=2 m T}\) exists vertically downwards. These magnetic field lines pass through a closed surface as shown in the figure. The closed surface consists of a hemisphere \({S_{1}}\), a right circular cone \({S_{2}}\) and a circular surface \({S_{3}}\). The magnetic flux through \({S_{1}}\) and \({S_{2}}\) are respectively
