360400 A bar magnet having a magnetic moment of \(2 \times {10^4}J{T^{ - 1}}\) is free to rotate in a horizontal plane. Ahorizontal magnetic field \(B = 6 \times {10^{ - 4}}\;T\) exists in thespace. The work done in taking the magnet slowlyfrom a direction parallel to the field to a direction \(60^{\circ}\) from the field is

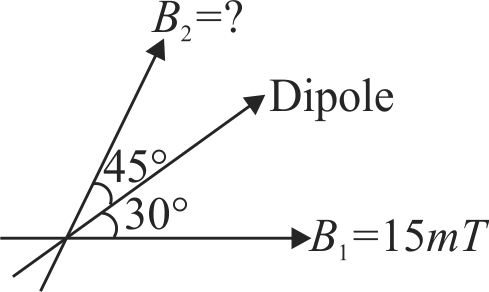
360401 A magnetic dipole is kept free in a region where two magnetic fields exist which are inclined to each other at an angle of \(75^{\circ}\). One of the fields has magnitude of 15 \(mT\). The dipole attains stable equilibrium at an angle \(30^{\circ}\) with this field. The magnitude of the other field (in \(mT\)) is close to :

360402 The work done in turning a magnet of magnetic moment \(M\) by an angle of \(90^{\circ}\) from the meridian, is \(n\) times the corresponding work done to turn it through an angle of \(30^{\circ}\). The value of ' \(n\) ' is

360403 Magnetic moment of bar magnet is \({M}\). The work done to turn the magnet by \({90^{\circ}}\) from the direction of magnetic field \({B}\) will be

360404 If the work done in turning a magnet of magnetic moment \(M\) by an angle of \(90^{\circ}\) from the magnetic meridian is \(n\) times the corresponding work done to turn it through an angle of \(60^{\circ}\), then the value of \(n\) is

360400 A bar magnet having a magnetic moment of \(2 \times {10^4}J{T^{ - 1}}\) is free to rotate in a horizontal plane. Ahorizontal magnetic field \(B = 6 \times {10^{ - 4}}\;T\) exists in thespace. The work done in taking the magnet slowlyfrom a direction parallel to the field to a direction \(60^{\circ}\) from the field is

360401 A magnetic dipole is kept free in a region where two magnetic fields exist which are inclined to each other at an angle of \(75^{\circ}\). One of the fields has magnitude of 15 \(mT\). The dipole attains stable equilibrium at an angle \(30^{\circ}\) with this field. The magnitude of the other field (in \(mT\)) is close to :

360402 The work done in turning a magnet of magnetic moment \(M\) by an angle of \(90^{\circ}\) from the meridian, is \(n\) times the corresponding work done to turn it through an angle of \(30^{\circ}\). The value of ' \(n\) ' is

360403 Magnetic moment of bar magnet is \({M}\). The work done to turn the magnet by \({90^{\circ}}\) from the direction of magnetic field \({B}\) will be

360404 If the work done in turning a magnet of magnetic moment \(M\) by an angle of \(90^{\circ}\) from the magnetic meridian is \(n\) times the corresponding work done to turn it through an angle of \(60^{\circ}\), then the value of \(n\) is

360400 A bar magnet having a magnetic moment of \(2 \times {10^4}J{T^{ - 1}}\) is free to rotate in a horizontal plane. Ahorizontal magnetic field \(B = 6 \times {10^{ - 4}}\;T\) exists in thespace. The work done in taking the magnet slowlyfrom a direction parallel to the field to a direction \(60^{\circ}\) from the field is

360401 A magnetic dipole is kept free in a region where two magnetic fields exist which are inclined to each other at an angle of \(75^{\circ}\). One of the fields has magnitude of 15 \(mT\). The dipole attains stable equilibrium at an angle \(30^{\circ}\) with this field. The magnitude of the other field (in \(mT\)) is close to :

360402 The work done in turning a magnet of magnetic moment \(M\) by an angle of \(90^{\circ}\) from the meridian, is \(n\) times the corresponding work done to turn it through an angle of \(30^{\circ}\). The value of ' \(n\) ' is

360403 Magnetic moment of bar magnet is \({M}\). The work done to turn the magnet by \({90^{\circ}}\) from the direction of magnetic field \({B}\) will be

360404 If the work done in turning a magnet of magnetic moment \(M\) by an angle of \(90^{\circ}\) from the magnetic meridian is \(n\) times the corresponding work done to turn it through an angle of \(60^{\circ}\), then the value of \(n\) is

360400 A bar magnet having a magnetic moment of \(2 \times {10^4}J{T^{ - 1}}\) is free to rotate in a horizontal plane. Ahorizontal magnetic field \(B = 6 \times {10^{ - 4}}\;T\) exists in thespace. The work done in taking the magnet slowlyfrom a direction parallel to the field to a direction \(60^{\circ}\) from the field is

360401 A magnetic dipole is kept free in a region where two magnetic fields exist which are inclined to each other at an angle of \(75^{\circ}\). One of the fields has magnitude of 15 \(mT\). The dipole attains stable equilibrium at an angle \(30^{\circ}\) with this field. The magnitude of the other field (in \(mT\)) is close to :

360402 The work done in turning a magnet of magnetic moment \(M\) by an angle of \(90^{\circ}\) from the meridian, is \(n\) times the corresponding work done to turn it through an angle of \(30^{\circ}\). The value of ' \(n\) ' is

360403 Magnetic moment of bar magnet is \({M}\). The work done to turn the magnet by \({90^{\circ}}\) from the direction of magnetic field \({B}\) will be

360404 If the work done in turning a magnet of magnetic moment \(M\) by an angle of \(90^{\circ}\) from the magnetic meridian is \(n\) times the corresponding work done to turn it through an angle of \(60^{\circ}\), then the value of \(n\) is

360400 A bar magnet having a magnetic moment of \(2 \times {10^4}J{T^{ - 1}}\) is free to rotate in a horizontal plane. Ahorizontal magnetic field \(B = 6 \times {10^{ - 4}}\;T\) exists in thespace. The work done in taking the magnet slowlyfrom a direction parallel to the field to a direction \(60^{\circ}\) from the field is

360401 A magnetic dipole is kept free in a region where two magnetic fields exist which are inclined to each other at an angle of \(75^{\circ}\). One of the fields has magnitude of 15 \(mT\). The dipole attains stable equilibrium at an angle \(30^{\circ}\) with this field. The magnitude of the other field (in \(mT\)) is close to :

360402 The work done in turning a magnet of magnetic moment \(M\) by an angle of \(90^{\circ}\) from the meridian, is \(n\) times the corresponding work done to turn it through an angle of \(30^{\circ}\). The value of ' \(n\) ' is

360403 Magnetic moment of bar magnet is \({M}\). The work done to turn the magnet by \({90^{\circ}}\) from the direction of magnetic field \({B}\) will be

360404 If the work done in turning a magnet of magnetic moment \(M\) by an angle of \(90^{\circ}\) from the magnetic meridian is \(n\) times the corresponding work done to turn it through an angle of \(60^{\circ}\), then the value of \(n\) is