360211
The mass of hydrogen molecules is
\(3.32 \times {10^{ - 27}} kg\). If \(10^{23}\) hydrogen molecules}
strike per second at on \(2\,\,c{m^2}\) area of a rigid wall at an angle of \(45^{\circ}\) from the normal and are rebound back with speed of \(1000\,\,m/s\), then the pressure exerted on the wall is (Assume collision is elastic)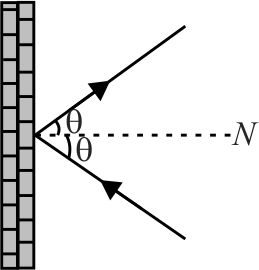
360212
\(10^{23}\) molecules of a gas, each having a mass of \(3 \times {10^{ - 27}}\;kg\) strike per second per sq. \(cm\) of a rigid wall at an angle of \(60^{\circ}\) with the normal and rebound with a velocity of \(500\;m{\rm{/}}s\). The pressure exerted by the gas molecules on the wall is
\(\left[ {\sin 30^\circ = \cos 60^\circ = 0.5,\cos 30^\circ = \sin 60^\circ = \sqrt 3 {\rm{/}}2} \right]\)
360211
The mass of hydrogen molecules is
\(3.32 \times {10^{ - 27}} kg\). If \(10^{23}\) hydrogen molecules}
strike per second at on \(2\,\,c{m^2}\) area of a rigid wall at an angle of \(45^{\circ}\) from the normal and are rebound back with speed of \(1000\,\,m/s\), then the pressure exerted on the wall is (Assume collision is elastic)
360212
\(10^{23}\) molecules of a gas, each having a mass of \(3 \times {10^{ - 27}}\;kg\) strike per second per sq. \(cm\) of a rigid wall at an angle of \(60^{\circ}\) with the normal and rebound with a velocity of \(500\;m{\rm{/}}s\). The pressure exerted by the gas molecules on the wall is
\(\left[ {\sin 30^\circ = \cos 60^\circ = 0.5,\cos 30^\circ = \sin 60^\circ = \sqrt 3 {\rm{/}}2} \right]\)
360211
The mass of hydrogen molecules is
\(3.32 \times {10^{ - 27}} kg\). If \(10^{23}\) hydrogen molecules}
strike per second at on \(2\,\,c{m^2}\) area of a rigid wall at an angle of \(45^{\circ}\) from the normal and are rebound back with speed of \(1000\,\,m/s\), then the pressure exerted on the wall is (Assume collision is elastic)
360212
\(10^{23}\) molecules of a gas, each having a mass of \(3 \times {10^{ - 27}}\;kg\) strike per second per sq. \(cm\) of a rigid wall at an angle of \(60^{\circ}\) with the normal and rebound with a velocity of \(500\;m{\rm{/}}s\). The pressure exerted by the gas molecules on the wall is
\(\left[ {\sin 30^\circ = \cos 60^\circ = 0.5,\cos 30^\circ = \sin 60^\circ = \sqrt 3 {\rm{/}}2} \right]\)
360211
The mass of hydrogen molecules is
\(3.32 \times {10^{ - 27}} kg\). If \(10^{23}\) hydrogen molecules}
strike per second at on \(2\,\,c{m^2}\) area of a rigid wall at an angle of \(45^{\circ}\) from the normal and are rebound back with speed of \(1000\,\,m/s\), then the pressure exerted on the wall is (Assume collision is elastic)
360212
\(10^{23}\) molecules of a gas, each having a mass of \(3 \times {10^{ - 27}}\;kg\) strike per second per sq. \(cm\) of a rigid wall at an angle of \(60^{\circ}\) with the normal and rebound with a velocity of \(500\;m{\rm{/}}s\). The pressure exerted by the gas molecules on the wall is
\(\left[ {\sin 30^\circ = \cos 60^\circ = 0.5,\cos 30^\circ = \sin 60^\circ = \sqrt 3 {\rm{/}}2} \right]\)
360211
The mass of hydrogen molecules is
\(3.32 \times {10^{ - 27}} kg\). If \(10^{23}\) hydrogen molecules}
strike per second at on \(2\,\,c{m^2}\) area of a rigid wall at an angle of \(45^{\circ}\) from the normal and are rebound back with speed of \(1000\,\,m/s\), then the pressure exerted on the wall is (Assume collision is elastic)
360212
\(10^{23}\) molecules of a gas, each having a mass of \(3 \times {10^{ - 27}}\;kg\) strike per second per sq. \(cm\) of a rigid wall at an angle of \(60^{\circ}\) with the normal and rebound with a velocity of \(500\;m{\rm{/}}s\). The pressure exerted by the gas molecules on the wall is
\(\left[ {\sin 30^\circ = \cos 60^\circ = 0.5,\cos 30^\circ = \sin 60^\circ = \sqrt 3 {\rm{/}}2} \right]\)

