360085
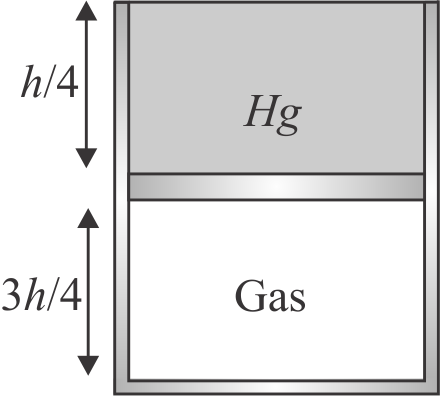
A vertical hollow cylinder of height \(1.52\,m\) is fitted with a movable piston of negligible mass and thickness. The lower part of cylinder contains an ideal gas and the upper part is filled with mercury as shown in figure. Initially the temperature of system is \(300\,K\) and the lengths of gas and mercury columns are equal. Find the temperature to which system is raised so that half of mercury overflows. Take atmospheric pressure \(76\,cm\) of \(Hg\) and neglect thermal expansion of mercury.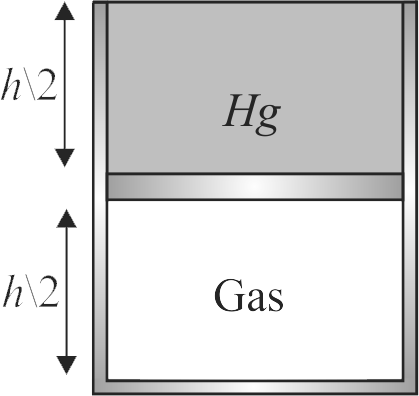
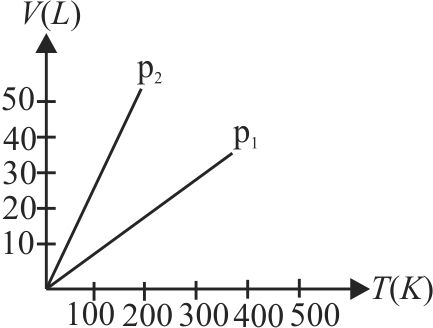
360086 Initially a gas of diatomic molecules is contained in a cylinder of volume \(V\) at a pressure \(P\) and temperature \(250 K\). Assuming that \(50 \%\) of the molecules get dissociated causing a change in number of moles. The pressure of the resulting gas at temperature \(1000 K\), when contained in a volume \(2 V\) is given by \({P_2}\). The ratio \({P_2}/{P_1}\) is-
360085
A vertical hollow cylinder of height \(1.52\,m\) is fitted with a movable piston of negligible mass and thickness. The lower part of cylinder contains an ideal gas and the upper part is filled with mercury as shown in figure. Initially the temperature of system is \(300\,K\) and the lengths of gas and mercury columns are equal. Find the temperature to which system is raised so that half of mercury overflows. Take atmospheric pressure \(76\,cm\) of \(Hg\) and neglect thermal expansion of mercury.
360086 Initially a gas of diatomic molecules is contained in a cylinder of volume \(V\) at a pressure \(P\) and temperature \(250 K\). Assuming that \(50 \%\) of the molecules get dissociated causing a change in number of moles. The pressure of the resulting gas at temperature \(1000 K\), when contained in a volume \(2 V\) is given by \({P_2}\). The ratio \({P_2}/{P_1}\) is-
360085
A vertical hollow cylinder of height \(1.52\,m\) is fitted with a movable piston of negligible mass and thickness. The lower part of cylinder contains an ideal gas and the upper part is filled with mercury as shown in figure. Initially the temperature of system is \(300\,K\) and the lengths of gas and mercury columns are equal. Find the temperature to which system is raised so that half of mercury overflows. Take atmospheric pressure \(76\,cm\) of \(Hg\) and neglect thermal expansion of mercury.
360086 Initially a gas of diatomic molecules is contained in a cylinder of volume \(V\) at a pressure \(P\) and temperature \(250 K\). Assuming that \(50 \%\) of the molecules get dissociated causing a change in number of moles. The pressure of the resulting gas at temperature \(1000 K\), when contained in a volume \(2 V\) is given by \({P_2}\). The ratio \({P_2}/{P_1}\) is-
360085
A vertical hollow cylinder of height \(1.52\,m\) is fitted with a movable piston of negligible mass and thickness. The lower part of cylinder contains an ideal gas and the upper part is filled with mercury as shown in figure. Initially the temperature of system is \(300\,K\) and the lengths of gas and mercury columns are equal. Find the temperature to which system is raised so that half of mercury overflows. Take atmospheric pressure \(76\,cm\) of \(Hg\) and neglect thermal expansion of mercury.
360086 Initially a gas of diatomic molecules is contained in a cylinder of volume \(V\) at a pressure \(P\) and temperature \(250 K\). Assuming that \(50 \%\) of the molecules get dissociated causing a change in number of moles. The pressure of the resulting gas at temperature \(1000 K\), when contained in a volume \(2 V\) is given by \({P_2}\). The ratio \({P_2}/{P_1}\) is-
360085
A vertical hollow cylinder of height \(1.52\,m\) is fitted with a movable piston of negligible mass and thickness. The lower part of cylinder contains an ideal gas and the upper part is filled with mercury as shown in figure. Initially the temperature of system is \(300\,K\) and the lengths of gas and mercury columns are equal. Find the temperature to which system is raised so that half of mercury overflows. Take atmospheric pressure \(76\,cm\) of \(Hg\) and neglect thermal expansion of mercury.
360086 Initially a gas of diatomic molecules is contained in a cylinder of volume \(V\) at a pressure \(P\) and temperature \(250 K\). Assuming that \(50 \%\) of the molecules get dissociated causing a change in number of moles. The pressure of the resulting gas at temperature \(1000 K\), when contained in a volume \(2 V\) is given by \({P_2}\). The ratio \({P_2}/{P_1}\) is-