355685 Read the Statement - A and Statement - B carefully to mark the correct options given below:
Statement A :
A truck and a car moving with same kinetic energy are brought to rest by applying breaks which provides equal retarding forces. Both come to rest in equal distance.
Statement B :
A car moving towards east takes a turn and moves towards north, the speed remains unchanged. The acceleration of the car is zero.

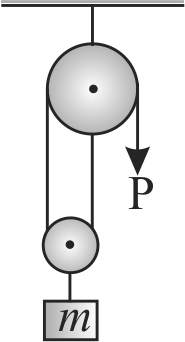
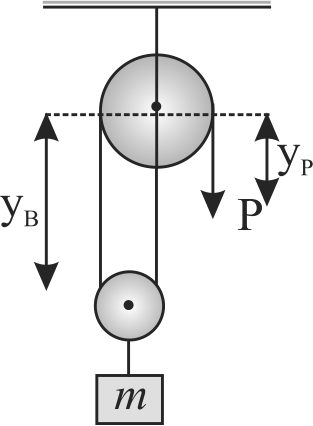
355686 A block of mass \(0.24\;kg\) is attached to a spring of force constant \(4\;N{\rm{/}}m.\) The coefficient of friction between the block and the floor is \(0.2.\) Initially the block is at rest and the spring is unstretched. An impulse is given to the block as shown in the figure. The block slides a distance of \(0.18\;m\) and comes to rest for the first time. The initial velocity of the block in \(m{\rm{/}}s\) is \(v = {\left( {\frac{N}{{100}}} \right)^{\frac{1}{2}}}\) then, \(N\) is (Take \(g = 10\;m{\rm{/}}{s^2}\) )

355687 For the situation shown in the given figure, the horizontal surface is rough. The coefficient of friction between the block of mass \({m_{1}=4 {~kg}}\) and the horizontal surface is \({\mu=0.5}\). The blocks are connected with combination of light spring of spring constant \({k}\) and a light string. The block of mass \({m_{2}}\) is released from rest, when spring is in its natural length. Find minimum value of \({m_{2}}\) such that the block of mass \({m_{1}}\) will start moving.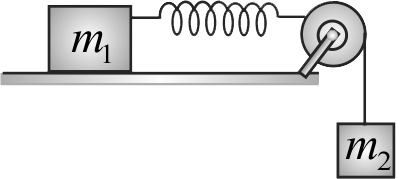

355688 When a bullet of mass \(10 \mathrm{~g}\) and speed \(100 \mathrm{~ms}^{-1}\) penetrates up to distance \(1 \mathrm{~cm}\) in a human body in rest. The resistance offered by human body is:

355689 The block of mass \(m\) is pulling, vertically up with constant speed, by applying force \(P\). The free end of the string is pulled by \(l\) meter, the increase in potential energy of the block is

355685 Read the Statement - A and Statement - B carefully to mark the correct options given below:
Statement A :
A truck and a car moving with same kinetic energy are brought to rest by applying breaks which provides equal retarding forces. Both come to rest in equal distance.
Statement B :
A car moving towards east takes a turn and moves towards north, the speed remains unchanged. The acceleration of the car is zero.

355686 A block of mass \(0.24\;kg\) is attached to a spring of force constant \(4\;N{\rm{/}}m.\) The coefficient of friction between the block and the floor is \(0.2.\) Initially the block is at rest and the spring is unstretched. An impulse is given to the block as shown in the figure. The block slides a distance of \(0.18\;m\) and comes to rest for the first time. The initial velocity of the block in \(m{\rm{/}}s\) is \(v = {\left( {\frac{N}{{100}}} \right)^{\frac{1}{2}}}\) then, \(N\) is (Take \(g = 10\;m{\rm{/}}{s^2}\) )

355687 For the situation shown in the given figure, the horizontal surface is rough. The coefficient of friction between the block of mass \({m_{1}=4 {~kg}}\) and the horizontal surface is \({\mu=0.5}\). The blocks are connected with combination of light spring of spring constant \({k}\) and a light string. The block of mass \({m_{2}}\) is released from rest, when spring is in its natural length. Find minimum value of \({m_{2}}\) such that the block of mass \({m_{1}}\) will start moving.

355688 When a bullet of mass \(10 \mathrm{~g}\) and speed \(100 \mathrm{~ms}^{-1}\) penetrates up to distance \(1 \mathrm{~cm}\) in a human body in rest. The resistance offered by human body is:

355689 The block of mass \(m\) is pulling, vertically up with constant speed, by applying force \(P\). The free end of the string is pulled by \(l\) meter, the increase in potential energy of the block is

355685 Read the Statement - A and Statement - B carefully to mark the correct options given below:
Statement A :
A truck and a car moving with same kinetic energy are brought to rest by applying breaks which provides equal retarding forces. Both come to rest in equal distance.
Statement B :
A car moving towards east takes a turn and moves towards north, the speed remains unchanged. The acceleration of the car is zero.

355686 A block of mass \(0.24\;kg\) is attached to a spring of force constant \(4\;N{\rm{/}}m.\) The coefficient of friction between the block and the floor is \(0.2.\) Initially the block is at rest and the spring is unstretched. An impulse is given to the block as shown in the figure. The block slides a distance of \(0.18\;m\) and comes to rest for the first time. The initial velocity of the block in \(m{\rm{/}}s\) is \(v = {\left( {\frac{N}{{100}}} \right)^{\frac{1}{2}}}\) then, \(N\) is (Take \(g = 10\;m{\rm{/}}{s^2}\) )

355687 For the situation shown in the given figure, the horizontal surface is rough. The coefficient of friction between the block of mass \({m_{1}=4 {~kg}}\) and the horizontal surface is \({\mu=0.5}\). The blocks are connected with combination of light spring of spring constant \({k}\) and a light string. The block of mass \({m_{2}}\) is released from rest, when spring is in its natural length. Find minimum value of \({m_{2}}\) such that the block of mass \({m_{1}}\) will start moving.

355688 When a bullet of mass \(10 \mathrm{~g}\) and speed \(100 \mathrm{~ms}^{-1}\) penetrates up to distance \(1 \mathrm{~cm}\) in a human body in rest. The resistance offered by human body is:

355689 The block of mass \(m\) is pulling, vertically up with constant speed, by applying force \(P\). The free end of the string is pulled by \(l\) meter, the increase in potential energy of the block is

355685 Read the Statement - A and Statement - B carefully to mark the correct options given below:
Statement A :
A truck and a car moving with same kinetic energy are brought to rest by applying breaks which provides equal retarding forces. Both come to rest in equal distance.
Statement B :
A car moving towards east takes a turn and moves towards north, the speed remains unchanged. The acceleration of the car is zero.

355686 A block of mass \(0.24\;kg\) is attached to a spring of force constant \(4\;N{\rm{/}}m.\) The coefficient of friction between the block and the floor is \(0.2.\) Initially the block is at rest and the spring is unstretched. An impulse is given to the block as shown in the figure. The block slides a distance of \(0.18\;m\) and comes to rest for the first time. The initial velocity of the block in \(m{\rm{/}}s\) is \(v = {\left( {\frac{N}{{100}}} \right)^{\frac{1}{2}}}\) then, \(N\) is (Take \(g = 10\;m{\rm{/}}{s^2}\) )

355687 For the situation shown in the given figure, the horizontal surface is rough. The coefficient of friction between the block of mass \({m_{1}=4 {~kg}}\) and the horizontal surface is \({\mu=0.5}\). The blocks are connected with combination of light spring of spring constant \({k}\) and a light string. The block of mass \({m_{2}}\) is released from rest, when spring is in its natural length. Find minimum value of \({m_{2}}\) such that the block of mass \({m_{1}}\) will start moving.

355688 When a bullet of mass \(10 \mathrm{~g}\) and speed \(100 \mathrm{~ms}^{-1}\) penetrates up to distance \(1 \mathrm{~cm}\) in a human body in rest. The resistance offered by human body is:

355689 The block of mass \(m\) is pulling, vertically up with constant speed, by applying force \(P\). The free end of the string is pulled by \(l\) meter, the increase in potential energy of the block is

355685 Read the Statement - A and Statement - B carefully to mark the correct options given below:
Statement A :
A truck and a car moving with same kinetic energy are brought to rest by applying breaks which provides equal retarding forces. Both come to rest in equal distance.
Statement B :
A car moving towards east takes a turn and moves towards north, the speed remains unchanged. The acceleration of the car is zero.

355686 A block of mass \(0.24\;kg\) is attached to a spring of force constant \(4\;N{\rm{/}}m.\) The coefficient of friction between the block and the floor is \(0.2.\) Initially the block is at rest and the spring is unstretched. An impulse is given to the block as shown in the figure. The block slides a distance of \(0.18\;m\) and comes to rest for the first time. The initial velocity of the block in \(m{\rm{/}}s\) is \(v = {\left( {\frac{N}{{100}}} \right)^{\frac{1}{2}}}\) then, \(N\) is (Take \(g = 10\;m{\rm{/}}{s^2}\) )

355687 For the situation shown in the given figure, the horizontal surface is rough. The coefficient of friction between the block of mass \({m_{1}=4 {~kg}}\) and the horizontal surface is \({\mu=0.5}\). The blocks are connected with combination of light spring of spring constant \({k}\) and a light string. The block of mass \({m_{2}}\) is released from rest, when spring is in its natural length. Find minimum value of \({m_{2}}\) such that the block of mass \({m_{1}}\) will start moving.

355688 When a bullet of mass \(10 \mathrm{~g}\) and speed \(100 \mathrm{~ms}^{-1}\) penetrates up to distance \(1 \mathrm{~cm}\) in a human body in rest. The resistance offered by human body is:

355689 The block of mass \(m\) is pulling, vertically up with constant speed, by applying force \(P\). The free end of the string is pulled by \(l\) meter, the increase in potential energy of the block is