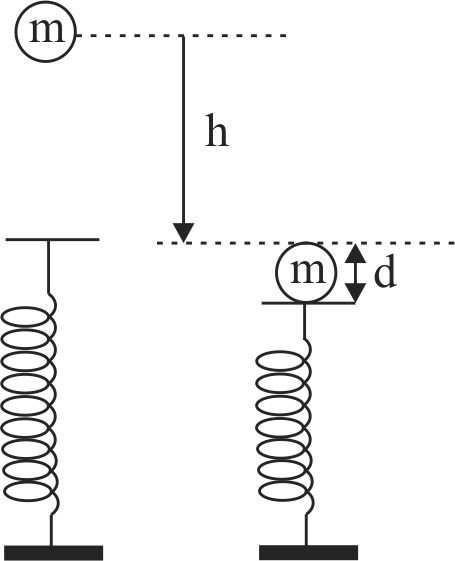
355608 A vertical spring with force constant \(K\) is fixed on a table. A ball of mass \(m\) at a height \(h\) above the free upper end of the spring falls vertically on the spring, so that the spring is compressed by a distance \(d\). The net work done by the spring in the process is
355610
A block of mass \(m\), lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant \(k\). The other end of the spring is fixed, as shown in the figure. The block is initially at rest in its equilibrium position. If now the block is pulled with a constant force \(F\), the maximum speed of the block is
355608 A vertical spring with force constant \(K\) is fixed on a table. A ball of mass \(m\) at a height \(h\) above the free upper end of the spring falls vertically on the spring, so that the spring is compressed by a distance \(d\). The net work done by the spring in the process is
355610
A block of mass \(m\), lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant \(k\). The other end of the spring is fixed, as shown in the figure. The block is initially at rest in its equilibrium position. If now the block is pulled with a constant force \(F\), the maximum speed of the block is
355608 A vertical spring with force constant \(K\) is fixed on a table. A ball of mass \(m\) at a height \(h\) above the free upper end of the spring falls vertically on the spring, so that the spring is compressed by a distance \(d\). The net work done by the spring in the process is
355610
A block of mass \(m\), lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant \(k\). The other end of the spring is fixed, as shown in the figure. The block is initially at rest in its equilibrium position. If now the block is pulled with a constant force \(F\), the maximum speed of the block is
355608 A vertical spring with force constant \(K\) is fixed on a table. A ball of mass \(m\) at a height \(h\) above the free upper end of the spring falls vertically on the spring, so that the spring is compressed by a distance \(d\). The net work done by the spring in the process is
355610
A block of mass \(m\), lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant \(k\). The other end of the spring is fixed, as shown in the figure. The block is initially at rest in its equilibrium position. If now the block is pulled with a constant force \(F\), the maximum speed of the block is
355608 A vertical spring with force constant \(K\) is fixed on a table. A ball of mass \(m\) at a height \(h\) above the free upper end of the spring falls vertically on the spring, so that the spring is compressed by a distance \(d\). The net work done by the spring in the process is
355610
A block of mass \(m\), lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant \(k\). The other end of the spring is fixed, as shown in the figure. The block is initially at rest in its equilibrium position. If now the block is pulled with a constant force \(F\), the maximum speed of the block is