355050 \(S_{1}\) and \(S_{2}\) are two coherent sources of sound having no initial phase difference. The velocity of sound is \(330\;m/s\). No minima will be formed on the line passing through \(S_{2}\) and perpendicular to the line joining \(S_{1}\) and \(S_{2}\), if the frequency of both the sources may be :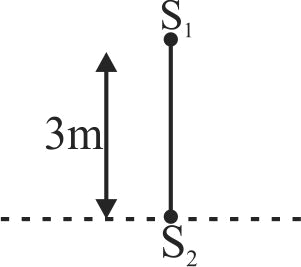

355051 Two sound waves, each of amplitude \(A\) and frequency \(\omega\) superpose at a point with phase difference of \(\dfrac{\pi}{2}\). The amplitude and frequency of the resultant wave are respectively

355052 The phenomena arising due to the superposition of waves is/are

355053 Sound signal is sent through a composite tube as shown in Fig. The radius of the semicircle is \(r\). Speed of sound in air is \(v\). The source of sound is capable to generate frequencies in the range \(f_{1}\) to \(f_{2}\left(f_{2}>f_{1}\right)\). If \(n\) is an integer then frequency for maximum intensity at ' \(p\) ' is given by

355054 The principle of superposition of waves can not be used to explain wave phenomena like

355050 \(S_{1}\) and \(S_{2}\) are two coherent sources of sound having no initial phase difference. The velocity of sound is \(330\;m/s\). No minima will be formed on the line passing through \(S_{2}\) and perpendicular to the line joining \(S_{1}\) and \(S_{2}\), if the frequency of both the sources may be :

355051 Two sound waves, each of amplitude \(A\) and frequency \(\omega\) superpose at a point with phase difference of \(\dfrac{\pi}{2}\). The amplitude and frequency of the resultant wave are respectively

355052 The phenomena arising due to the superposition of waves is/are

355053 Sound signal is sent through a composite tube as shown in Fig. The radius of the semicircle is \(r\). Speed of sound in air is \(v\). The source of sound is capable to generate frequencies in the range \(f_{1}\) to \(f_{2}\left(f_{2}>f_{1}\right)\). If \(n\) is an integer then frequency for maximum intensity at ' \(p\) ' is given by

355054 The principle of superposition of waves can not be used to explain wave phenomena like

355050 \(S_{1}\) and \(S_{2}\) are two coherent sources of sound having no initial phase difference. The velocity of sound is \(330\;m/s\). No minima will be formed on the line passing through \(S_{2}\) and perpendicular to the line joining \(S_{1}\) and \(S_{2}\), if the frequency of both the sources may be :

355051 Two sound waves, each of amplitude \(A\) and frequency \(\omega\) superpose at a point with phase difference of \(\dfrac{\pi}{2}\). The amplitude and frequency of the resultant wave are respectively

355052 The phenomena arising due to the superposition of waves is/are

355053 Sound signal is sent through a composite tube as shown in Fig. The radius of the semicircle is \(r\). Speed of sound in air is \(v\). The source of sound is capable to generate frequencies in the range \(f_{1}\) to \(f_{2}\left(f_{2}>f_{1}\right)\). If \(n\) is an integer then frequency for maximum intensity at ' \(p\) ' is given by

355054 The principle of superposition of waves can not be used to explain wave phenomena like

355050 \(S_{1}\) and \(S_{2}\) are two coherent sources of sound having no initial phase difference. The velocity of sound is \(330\;m/s\). No minima will be formed on the line passing through \(S_{2}\) and perpendicular to the line joining \(S_{1}\) and \(S_{2}\), if the frequency of both the sources may be :

355051 Two sound waves, each of amplitude \(A\) and frequency \(\omega\) superpose at a point with phase difference of \(\dfrac{\pi}{2}\). The amplitude and frequency of the resultant wave are respectively

355052 The phenomena arising due to the superposition of waves is/are

355053 Sound signal is sent through a composite tube as shown in Fig. The radius of the semicircle is \(r\). Speed of sound in air is \(v\). The source of sound is capable to generate frequencies in the range \(f_{1}\) to \(f_{2}\left(f_{2}>f_{1}\right)\). If \(n\) is an integer then frequency for maximum intensity at ' \(p\) ' is given by

355054 The principle of superposition of waves can not be used to explain wave phenomena like

355050 \(S_{1}\) and \(S_{2}\) are two coherent sources of sound having no initial phase difference. The velocity of sound is \(330\;m/s\). No minima will be formed on the line passing through \(S_{2}\) and perpendicular to the line joining \(S_{1}\) and \(S_{2}\), if the frequency of both the sources may be :

355051 Two sound waves, each of amplitude \(A\) and frequency \(\omega\) superpose at a point with phase difference of \(\dfrac{\pi}{2}\). The amplitude and frequency of the resultant wave are respectively

355052 The phenomena arising due to the superposition of waves is/are

355053 Sound signal is sent through a composite tube as shown in Fig. The radius of the semicircle is \(r\). Speed of sound in air is \(v\). The source of sound is capable to generate frequencies in the range \(f_{1}\) to \(f_{2}\left(f_{2}>f_{1}\right)\). If \(n\) is an integer then frequency for maximum intensity at ' \(p\) ' is given by

355054 The principle of superposition of waves can not be used to explain wave phenomena like