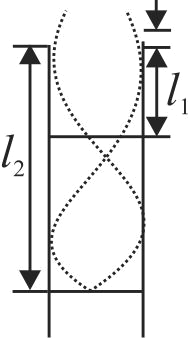
354910 A pipe closed at one end has length \(0.8\;m\). At its open end a \(0.5\;m\) long uniform string is vibrating in its second harmonic and it resonates with the fundamental frequency of the pipe. If the tension in the wire in \(50\;N\) and the speed of sound is \(320\;m{\rm{/}}s\), the mass of the string used is
354910 A pipe closed at one end has length \(0.8\;m\). At its open end a \(0.5\;m\) long uniform string is vibrating in its second harmonic and it resonates with the fundamental frequency of the pipe. If the tension in the wire in \(50\;N\) and the speed of sound is \(320\;m{\rm{/}}s\), the mass of the string used is
354910 A pipe closed at one end has length \(0.8\;m\). At its open end a \(0.5\;m\) long uniform string is vibrating in its second harmonic and it resonates with the fundamental frequency of the pipe. If the tension in the wire in \(50\;N\) and the speed of sound is \(320\;m{\rm{/}}s\), the mass of the string used is
354910 A pipe closed at one end has length \(0.8\;m\). At its open end a \(0.5\;m\) long uniform string is vibrating in its second harmonic and it resonates with the fundamental frequency of the pipe. If the tension in the wire in \(50\;N\) and the speed of sound is \(320\;m{\rm{/}}s\), the mass of the string used is
354910 A pipe closed at one end has length \(0.8\;m\). At its open end a \(0.5\;m\) long uniform string is vibrating in its second harmonic and it resonates with the fundamental frequency of the pipe. If the tension in the wire in \(50\;N\) and the speed of sound is \(320\;m{\rm{/}}s\), the mass of the string used is