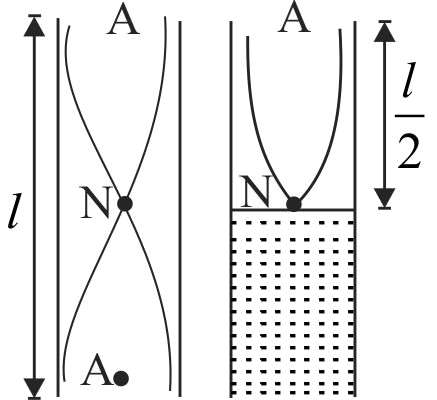
354947 A glass tube is open at both the ends. A tuning fork of frequency \(f\) resonates with the air column inside the tube. Now the tube is placed vertically inside water so that half the length of the tube is filled with water. Now the air column inside the tube is in unison with another fork of frequency \(f^{\prime}\). Then
354947 A glass tube is open at both the ends. A tuning fork of frequency \(f\) resonates with the air column inside the tube. Now the tube is placed vertically inside water so that half the length of the tube is filled with water. Now the air column inside the tube is in unison with another fork of frequency \(f^{\prime}\). Then
354947 A glass tube is open at both the ends. A tuning fork of frequency \(f\) resonates with the air column inside the tube. Now the tube is placed vertically inside water so that half the length of the tube is filled with water. Now the air column inside the tube is in unison with another fork of frequency \(f^{\prime}\). Then
354947 A glass tube is open at both the ends. A tuning fork of frequency \(f\) resonates with the air column inside the tube. Now the tube is placed vertically inside water so that half the length of the tube is filled with water. Now the air column inside the tube is in unison with another fork of frequency \(f^{\prime}\). Then