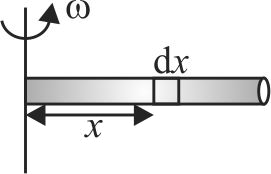
354836 A uniform string of length \(l\), mass \(M\) rotates about one of its end \(O\) in a horizontal plane with an angular speed \(\omega\). You can ignore force of gravity on the string. The time taken by a transverse wave pulse from one end of the string to another i.e., \(O\) is \(\dfrac{\pi}{\sqrt{x} . \omega}\). The value of \(x\) is

354837 Two blocks each having a mass of \(3.2\;kg\) are connected by a wire \(CD\) and the system is suspended from the ceiling by another wire \(AB\). The linear mass density of the wire \(AB\) is \(10gm/m\) and that of \(CD\) is \(8gm/m\). The ratio of wave speeds in strings \(AB,CD\) is \(\sqrt{\dfrac{8}{x}}\). The value of \(x\) is

354838 A transverse wave propagating on a stretched string of linear density \(3 \times {10^{ - 2}}\;kg - {m^{ - 1}}\) is represented by the equation \(y=0.2 \sin (1.5 x+60 t)\). Where, \(x\) is in meters and \(t\) is in seconds. The tension in the string (in newton) is:

354839 \(\lambda\) is maximum wavelength of a transverse wave that travels along a stretched wire whose two ends are fixed. The length of that wire is

354840 A string of mass \(2.5\;kg\) is under a tension of 200 \(N\). The length of the stretched string is \(20.0\;m\). If the transverse jerk is struck at one end of the string, the disturbance will reach the other end in

354836 A uniform string of length \(l\), mass \(M\) rotates about one of its end \(O\) in a horizontal plane with an angular speed \(\omega\). You can ignore force of gravity on the string. The time taken by a transverse wave pulse from one end of the string to another i.e., \(O\) is \(\dfrac{\pi}{\sqrt{x} . \omega}\). The value of \(x\) is

354837 Two blocks each having a mass of \(3.2\;kg\) are connected by a wire \(CD\) and the system is suspended from the ceiling by another wire \(AB\). The linear mass density of the wire \(AB\) is \(10gm/m\) and that of \(CD\) is \(8gm/m\). The ratio of wave speeds in strings \(AB,CD\) is \(\sqrt{\dfrac{8}{x}}\). The value of \(x\) is

354838 A transverse wave propagating on a stretched string of linear density \(3 \times {10^{ - 2}}\;kg - {m^{ - 1}}\) is represented by the equation \(y=0.2 \sin (1.5 x+60 t)\). Where, \(x\) is in meters and \(t\) is in seconds. The tension in the string (in newton) is:

354839 \(\lambda\) is maximum wavelength of a transverse wave that travels along a stretched wire whose two ends are fixed. The length of that wire is

354840 A string of mass \(2.5\;kg\) is under a tension of 200 \(N\). The length of the stretched string is \(20.0\;m\). If the transverse jerk is struck at one end of the string, the disturbance will reach the other end in

354836 A uniform string of length \(l\), mass \(M\) rotates about one of its end \(O\) in a horizontal plane with an angular speed \(\omega\). You can ignore force of gravity on the string. The time taken by a transverse wave pulse from one end of the string to another i.e., \(O\) is \(\dfrac{\pi}{\sqrt{x} . \omega}\). The value of \(x\) is

354837 Two blocks each having a mass of \(3.2\;kg\) are connected by a wire \(CD\) and the system is suspended from the ceiling by another wire \(AB\). The linear mass density of the wire \(AB\) is \(10gm/m\) and that of \(CD\) is \(8gm/m\). The ratio of wave speeds in strings \(AB,CD\) is \(\sqrt{\dfrac{8}{x}}\). The value of \(x\) is

354838 A transverse wave propagating on a stretched string of linear density \(3 \times {10^{ - 2}}\;kg - {m^{ - 1}}\) is represented by the equation \(y=0.2 \sin (1.5 x+60 t)\). Where, \(x\) is in meters and \(t\) is in seconds. The tension in the string (in newton) is:

354839 \(\lambda\) is maximum wavelength of a transverse wave that travels along a stretched wire whose two ends are fixed. The length of that wire is

354840 A string of mass \(2.5\;kg\) is under a tension of 200 \(N\). The length of the stretched string is \(20.0\;m\). If the transverse jerk is struck at one end of the string, the disturbance will reach the other end in

354836 A uniform string of length \(l\), mass \(M\) rotates about one of its end \(O\) in a horizontal plane with an angular speed \(\omega\). You can ignore force of gravity on the string. The time taken by a transverse wave pulse from one end of the string to another i.e., \(O\) is \(\dfrac{\pi}{\sqrt{x} . \omega}\). The value of \(x\) is

354837 Two blocks each having a mass of \(3.2\;kg\) are connected by a wire \(CD\) and the system is suspended from the ceiling by another wire \(AB\). The linear mass density of the wire \(AB\) is \(10gm/m\) and that of \(CD\) is \(8gm/m\). The ratio of wave speeds in strings \(AB,CD\) is \(\sqrt{\dfrac{8}{x}}\). The value of \(x\) is

354838 A transverse wave propagating on a stretched string of linear density \(3 \times {10^{ - 2}}\;kg - {m^{ - 1}}\) is represented by the equation \(y=0.2 \sin (1.5 x+60 t)\). Where, \(x\) is in meters and \(t\) is in seconds. The tension in the string (in newton) is:

354839 \(\lambda\) is maximum wavelength of a transverse wave that travels along a stretched wire whose two ends are fixed. The length of that wire is

354840 A string of mass \(2.5\;kg\) is under a tension of 200 \(N\). The length of the stretched string is \(20.0\;m\). If the transverse jerk is struck at one end of the string, the disturbance will reach the other end in

354836 A uniform string of length \(l\), mass \(M\) rotates about one of its end \(O\) in a horizontal plane with an angular speed \(\omega\). You can ignore force of gravity on the string. The time taken by a transverse wave pulse from one end of the string to another i.e., \(O\) is \(\dfrac{\pi}{\sqrt{x} . \omega}\). The value of \(x\) is

354837 Two blocks each having a mass of \(3.2\;kg\) are connected by a wire \(CD\) and the system is suspended from the ceiling by another wire \(AB\). The linear mass density of the wire \(AB\) is \(10gm/m\) and that of \(CD\) is \(8gm/m\). The ratio of wave speeds in strings \(AB,CD\) is \(\sqrt{\dfrac{8}{x}}\). The value of \(x\) is

354838 A transverse wave propagating on a stretched string of linear density \(3 \times {10^{ - 2}}\;kg - {m^{ - 1}}\) is represented by the equation \(y=0.2 \sin (1.5 x+60 t)\). Where, \(x\) is in meters and \(t\) is in seconds. The tension in the string (in newton) is:

354839 \(\lambda\) is maximum wavelength of a transverse wave that travels along a stretched wire whose two ends are fixed. The length of that wire is

354840 A string of mass \(2.5\;kg\) is under a tension of 200 \(N\). The length of the stretched string is \(20.0\;m\). If the transverse jerk is struck at one end of the string, the disturbance will reach the other end in