Explanation:
In fundamental mode,
\(l=2\left(\dfrac{\lambda}{4}\right)=\dfrac{\lambda}{2}\)
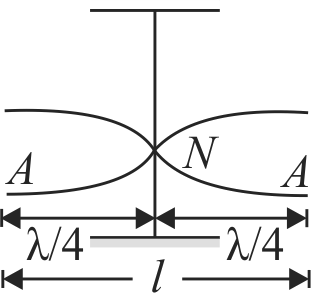
\( \Rightarrow \lambda = 2l\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
Given, \(l = 100\;cm\),
\(v = 2.53\,kHz = 2.53 \times {10^3}\;Hz\)
We know that,
\(v=v \lambda\)
\(=v \times 2 l \quad[\) From Eq. (1) ]
\(=2.53 \times 10^{3} \times 2 \times 100 \times 10^{-2}\)
\( = 5.06 \times {10^3}\;m{s^{ - 1}}\)
\( = 5.06\,km{s^{ - 1}}\)