354559
A longitudinal harmonic wave is travelling along positive \(x\) direction. The amplitude, wavelength and frequency of the wave are \(8.0 \times 10^{-3} {~m}, 12 {~cm}\) and 6800 \(Hz\) respectively. The displacement (\(s\)) versus position graph for particles on the \(x\)-axis at an instant of time has been shown in the figure. Find the separation at the instant shown, between the particles which were originally at \(x_{1}=1 {~cm}\) and \(x_{2}=3 {~cm}\).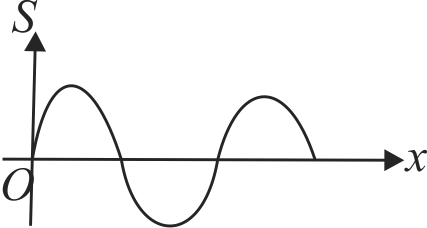
354559
A longitudinal harmonic wave is travelling along positive \(x\) direction. The amplitude, wavelength and frequency of the wave are \(8.0 \times 10^{-3} {~m}, 12 {~cm}\) and 6800 \(Hz\) respectively. The displacement (\(s\)) versus position graph for particles on the \(x\)-axis at an instant of time has been shown in the figure. Find the separation at the instant shown, between the particles which were originally at \(x_{1}=1 {~cm}\) and \(x_{2}=3 {~cm}\).
354559
A longitudinal harmonic wave is travelling along positive \(x\) direction. The amplitude, wavelength and frequency of the wave are \(8.0 \times 10^{-3} {~m}, 12 {~cm}\) and 6800 \(Hz\) respectively. The displacement (\(s\)) versus position graph for particles on the \(x\)-axis at an instant of time has been shown in the figure. Find the separation at the instant shown, between the particles which were originally at \(x_{1}=1 {~cm}\) and \(x_{2}=3 {~cm}\).
354559
A longitudinal harmonic wave is travelling along positive \(x\) direction. The amplitude, wavelength and frequency of the wave are \(8.0 \times 10^{-3} {~m}, 12 {~cm}\) and 6800 \(Hz\) respectively. The displacement (\(s\)) versus position graph for particles on the \(x\)-axis at an instant of time has been shown in the figure. Find the separation at the instant shown, between the particles which were originally at \(x_{1}=1 {~cm}\) and \(x_{2}=3 {~cm}\).
