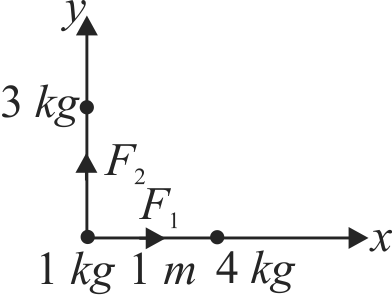
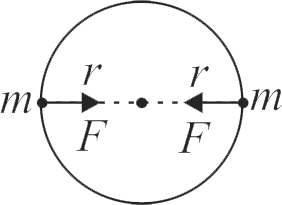
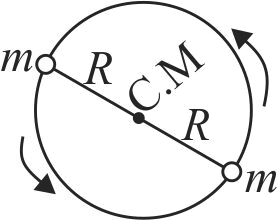
360043
In both figures shown below a hole is present along the diameter of earth. In first, a particle is released from \(A\) and it oscillated with time period \(T_{1}\). In second figure, same particle is relased from point \(B\) and it oscillates with time period \(T_{2}\) then [ \(O\) is centre of earth]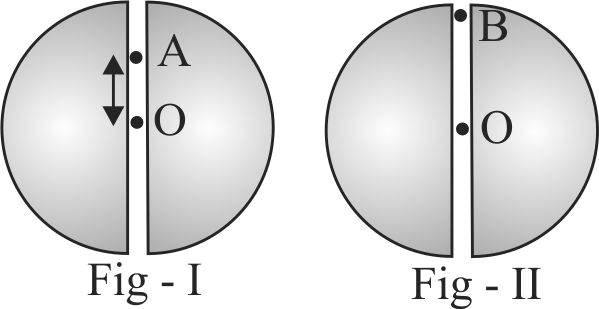
360043
In both figures shown below a hole is present along the diameter of earth. In first, a particle is released from \(A\) and it oscillated with time period \(T_{1}\). In second figure, same particle is relased from point \(B\) and it oscillates with time period \(T_{2}\) then [ \(O\) is centre of earth]
360043
In both figures shown below a hole is present along the diameter of earth. In first, a particle is released from \(A\) and it oscillated with time period \(T_{1}\). In second figure, same particle is relased from point \(B\) and it oscillates with time period \(T_{2}\) then [ \(O\) is centre of earth]
360043
In both figures shown below a hole is present along the diameter of earth. In first, a particle is released from \(A\) and it oscillated with time period \(T_{1}\). In second figure, same particle is relased from point \(B\) and it oscillates with time period \(T_{2}\) then [ \(O\) is centre of earth]
360043
In both figures shown below a hole is present along the diameter of earth. In first, a particle is released from \(A\) and it oscillated with time period \(T_{1}\). In second figure, same particle is relased from point \(B\) and it oscillates with time period \(T_{2}\) then [ \(O\) is centre of earth]