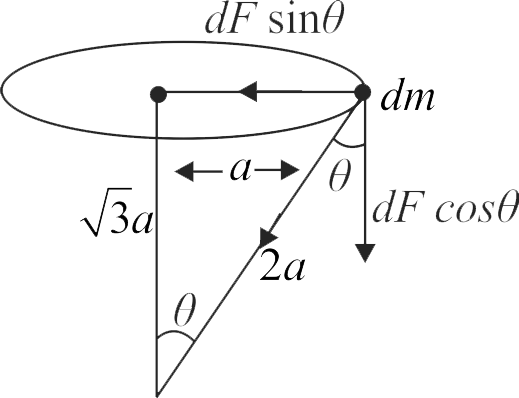
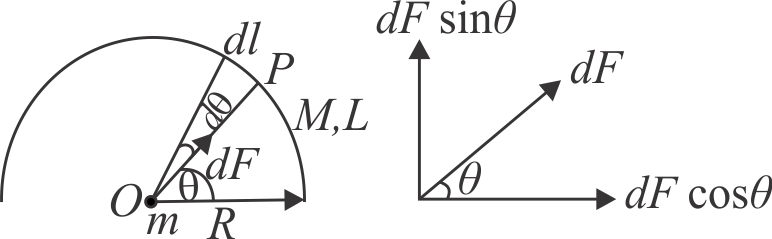360010 A uniform ring of mass \(2 m\) and radius ' \(a\) ' is placed directly above a uniform sphere of mass \(M\) and of equal radius. The centre of ring is at distance \(\sqrt 3 a\) from the centre of sphere. The gravitational force exerted by the sphere on the ring is \(N\frac{{GMm}}{{{a^2}}}\) units. What is the value of \(N\) ?
360010 A uniform ring of mass \(2 m\) and radius ' \(a\) ' is placed directly above a uniform sphere of mass \(M\) and of equal radius. The centre of ring is at distance \(\sqrt 3 a\) from the centre of sphere. The gravitational force exerted by the sphere on the ring is \(N\frac{{GMm}}{{{a^2}}}\) units. What is the value of \(N\) ?
360010 A uniform ring of mass \(2 m\) and radius ' \(a\) ' is placed directly above a uniform sphere of mass \(M\) and of equal radius. The centre of ring is at distance \(\sqrt 3 a\) from the centre of sphere. The gravitational force exerted by the sphere on the ring is \(N\frac{{GMm}}{{{a^2}}}\) units. What is the value of \(N\) ?
360010 A uniform ring of mass \(2 m\) and radius ' \(a\) ' is placed directly above a uniform sphere of mass \(M\) and of equal radius. The centre of ring is at distance \(\sqrt 3 a\) from the centre of sphere. The gravitational force exerted by the sphere on the ring is \(N\frac{{GMm}}{{{a^2}}}\) units. What is the value of \(N\) ?
360010 A uniform ring of mass \(2 m\) and radius ' \(a\) ' is placed directly above a uniform sphere of mass \(M\) and of equal radius. The centre of ring is at distance \(\sqrt 3 a\) from the centre of sphere. The gravitational force exerted by the sphere on the ring is \(N\frac{{GMm}}{{{a^2}}}\) units. What is the value of \(N\) ?