359780
If the law of gravitation be such that the force of attraction between two particles vary inversely as the \(5/{2^{th}}\) power of their separation, then the graph of orbital velocity \(v_{0}\) plotted against the distance \(r\) of a satellite from the earth's centre on a log-log scale is shown along side. The slope of line will be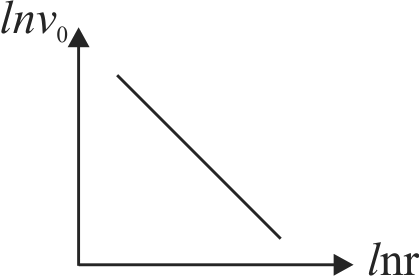
359780
If the law of gravitation be such that the force of attraction between two particles vary inversely as the \(5/{2^{th}}\) power of their separation, then the graph of orbital velocity \(v_{0}\) plotted against the distance \(r\) of a satellite from the earth's centre on a log-log scale is shown along side. The slope of line will be
359780
If the law of gravitation be such that the force of attraction between two particles vary inversely as the \(5/{2^{th}}\) power of their separation, then the graph of orbital velocity \(v_{0}\) plotted against the distance \(r\) of a satellite from the earth's centre on a log-log scale is shown along side. The slope of line will be
359780
If the law of gravitation be such that the force of attraction between two particles vary inversely as the \(5/{2^{th}}\) power of their separation, then the graph of orbital velocity \(v_{0}\) plotted against the distance \(r\) of a satellite from the earth's centre on a log-log scale is shown along side. The slope of line will be