359766
A triple star system consists of two stars, each of mass \(m\), in the same circular orbit about central star with mass \(M = 2 \times {10^{30}}\;kg\). The two outer stars always lie at opposite ends of a diameter of their common circular orbit. The radius of the circular orbit is \(r = {10^{11}}\;m\) and the orbital period of each star is \(1.6 \times 10^{7} s\).\(\left[ {Take{\text{ }}{\pi ^2} = 10\,and{\text{ }}G = \frac{{20}}{3} \times {{10}^{ - 11}}N{m^2}\;k{g^{ - 2}}} \right]\). The orbital velocity of each star is
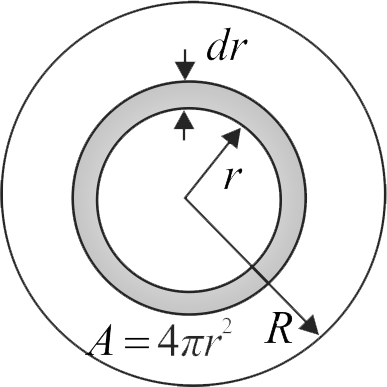
359768 A test particle is moving in a circular orbit in the gravitational field produced by a mass-density \(\rho (r) = \frac{k}{{{r^2}}},\) where \(k\) is a constant. The relation between the radius \(R\) of particle's orbit and its period \(T\) is found to be \(T^{N} R^{M}=\) constant. What is the value of \(N + M\)?
359766
A triple star system consists of two stars, each of mass \(m\), in the same circular orbit about central star with mass \(M = 2 \times {10^{30}}\;kg\). The two outer stars always lie at opposite ends of a diameter of their common circular orbit. The radius of the circular orbit is \(r = {10^{11}}\;m\) and the orbital period of each star is \(1.6 \times 10^{7} s\).\(\left[ {Take{\text{ }}{\pi ^2} = 10\,and{\text{ }}G = \frac{{20}}{3} \times {{10}^{ - 11}}N{m^2}\;k{g^{ - 2}}} \right]\). The orbital velocity of each star is
359768 A test particle is moving in a circular orbit in the gravitational field produced by a mass-density \(\rho (r) = \frac{k}{{{r^2}}},\) where \(k\) is a constant. The relation between the radius \(R\) of particle's orbit and its period \(T\) is found to be \(T^{N} R^{M}=\) constant. What is the value of \(N + M\)?
359766
A triple star system consists of two stars, each of mass \(m\), in the same circular orbit about central star with mass \(M = 2 \times {10^{30}}\;kg\). The two outer stars always lie at opposite ends of a diameter of their common circular orbit. The radius of the circular orbit is \(r = {10^{11}}\;m\) and the orbital period of each star is \(1.6 \times 10^{7} s\).\(\left[ {Take{\text{ }}{\pi ^2} = 10\,and{\text{ }}G = \frac{{20}}{3} \times {{10}^{ - 11}}N{m^2}\;k{g^{ - 2}}} \right]\). The orbital velocity of each star is
359768 A test particle is moving in a circular orbit in the gravitational field produced by a mass-density \(\rho (r) = \frac{k}{{{r^2}}},\) where \(k\) is a constant. The relation between the radius \(R\) of particle's orbit and its period \(T\) is found to be \(T^{N} R^{M}=\) constant. What is the value of \(N + M\)?
359766
A triple star system consists of two stars, each of mass \(m\), in the same circular orbit about central star with mass \(M = 2 \times {10^{30}}\;kg\). The two outer stars always lie at opposite ends of a diameter of their common circular orbit. The radius of the circular orbit is \(r = {10^{11}}\;m\) and the orbital period of each star is \(1.6 \times 10^{7} s\).\(\left[ {Take{\text{ }}{\pi ^2} = 10\,and{\text{ }}G = \frac{{20}}{3} \times {{10}^{ - 11}}N{m^2}\;k{g^{ - 2}}} \right]\). The orbital velocity of each star is
359768 A test particle is moving in a circular orbit in the gravitational field produced by a mass-density \(\rho (r) = \frac{k}{{{r^2}}},\) where \(k\) is a constant. The relation between the radius \(R\) of particle's orbit and its period \(T\) is found to be \(T^{N} R^{M}=\) constant. What is the value of \(N + M\)?