359587
Suppose, the acceleration due to gravity at the earth's surface is \(10\;m/{s^2}\) and at the surface of mars it is \(4.0 \mathrm{~m} / \mathrm{s}^{2}\). A \(4.0\;m/{s^2}\) passenger goes from the earth to the Mars in a spaceship moving with a constant velocity. Neglect all other objects in the sky.
Which part of figure best represents the weight ( net gravitational force ) of the passenger as a function of time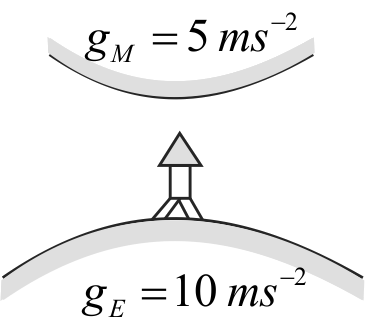
359587
Suppose, the acceleration due to gravity at the earth's surface is \(10\;m/{s^2}\) and at the surface of mars it is \(4.0 \mathrm{~m} / \mathrm{s}^{2}\). A \(4.0\;m/{s^2}\) passenger goes from the earth to the Mars in a spaceship moving with a constant velocity. Neglect all other objects in the sky.
Which part of figure best represents the weight ( net gravitational force ) of the passenger as a function of time
359587
Suppose, the acceleration due to gravity at the earth's surface is \(10\;m/{s^2}\) and at the surface of mars it is \(4.0 \mathrm{~m} / \mathrm{s}^{2}\). A \(4.0\;m/{s^2}\) passenger goes from the earth to the Mars in a spaceship moving with a constant velocity. Neglect all other objects in the sky.
Which part of figure best represents the weight ( net gravitational force ) of the passenger as a function of time
359587
Suppose, the acceleration due to gravity at the earth's surface is \(10\;m/{s^2}\) and at the surface of mars it is \(4.0 \mathrm{~m} / \mathrm{s}^{2}\). A \(4.0\;m/{s^2}\) passenger goes from the earth to the Mars in a spaceship moving with a constant velocity. Neglect all other objects in the sky.
Which part of figure best represents the weight ( net gravitational force ) of the passenger as a function of time