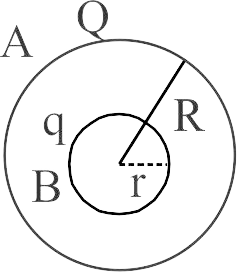359439
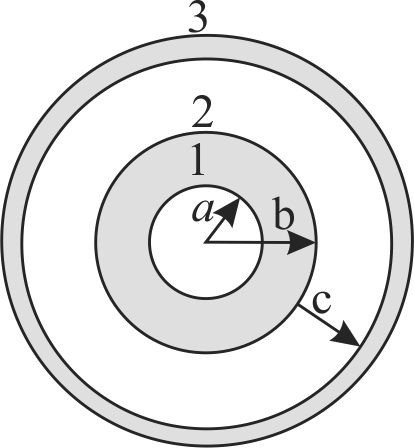
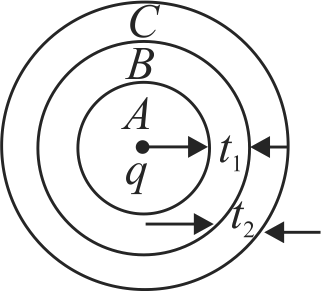
Three concentric conducting spherical shells have radii \(r\),\(2r\) and \(3r\) and charges \({q_1},{q_2}\) and \({q_3}\) respectively. The innermost and outermost shells are earthed as shown in the figure. The charges given are after earthing. Select the correct alternative.
359441 A small conducting sphere lying concentrically inside a bigger hollow conducting sphere of radius \(R\). The bigger and smaller spheres are charged with \(Q\) and \(q(Q > q)\) and are insulated from each other, The potential difference between the spheres will be
359439
Three concentric conducting spherical shells have radii \(r\),\(2r\) and \(3r\) and charges \({q_1},{q_2}\) and \({q_3}\) respectively. The innermost and outermost shells are earthed as shown in the figure. The charges given are after earthing. Select the correct alternative.
359441 A small conducting sphere lying concentrically inside a bigger hollow conducting sphere of radius \(R\). The bigger and smaller spheres are charged with \(Q\) and \(q(Q > q)\) and are insulated from each other, The potential difference between the spheres will be
359439
Three concentric conducting spherical shells have radii \(r\),\(2r\) and \(3r\) and charges \({q_1},{q_2}\) and \({q_3}\) respectively. The innermost and outermost shells are earthed as shown in the figure. The charges given are after earthing. Select the correct alternative.
359441 A small conducting sphere lying concentrically inside a bigger hollow conducting sphere of radius \(R\). The bigger and smaller spheres are charged with \(Q\) and \(q(Q > q)\) and are insulated from each other, The potential difference between the spheres will be
359439
Three concentric conducting spherical shells have radii \(r\),\(2r\) and \(3r\) and charges \({q_1},{q_2}\) and \({q_3}\) respectively. The innermost and outermost shells are earthed as shown in the figure. The charges given are after earthing. Select the correct alternative.
359441 A small conducting sphere lying concentrically inside a bigger hollow conducting sphere of radius \(R\). The bigger and smaller spheres are charged with \(Q\) and \(q(Q > q)\) and are insulated from each other, The potential difference between the spheres will be
359439
Three concentric conducting spherical shells have radii \(r\),\(2r\) and \(3r\) and charges \({q_1},{q_2}\) and \({q_3}\) respectively. The innermost and outermost shells are earthed as shown in the figure. The charges given are after earthing. Select the correct alternative.
359441 A small conducting sphere lying concentrically inside a bigger hollow conducting sphere of radius \(R\). The bigger and smaller spheres are charged with \(Q\) and \(q(Q > q)\) and are insulated from each other, The potential difference between the spheres will be