359423
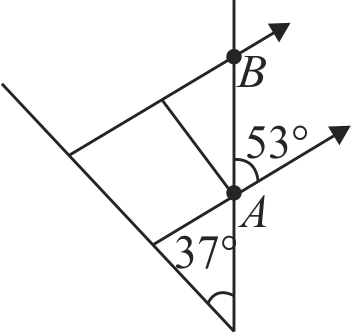
An infinite plane of charge with \({\sigma=2 \epsilon_{0} \dfrac{{C}}{{m}^{2}}}\) is tilted at a \({37^{\circ}}\) angle to the vertical direction as shown below. Find the potential difference, \({V_{A}-V_{B}}\) in volts, between points \({A}\) and \({B}\) at 5 \(m\) distance apart (where \({B}\) is vertically above \(A\,).\)
359425
A unit positive point charge of mass m is projected with a velocity \(v\) inside the tunnel which is made inside a uniformly charged non-conducting sphere of charge density \(\rho .\) The minimum velocity with which the point charge should be projected such that it can reach the opposite end of the tunnel, is equal to: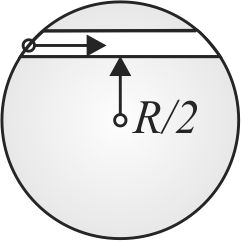
359423
An infinite plane of charge with \({\sigma=2 \epsilon_{0} \dfrac{{C}}{{m}^{2}}}\) is tilted at a \({37^{\circ}}\) angle to the vertical direction as shown below. Find the potential difference, \({V_{A}-V_{B}}\) in volts, between points \({A}\) and \({B}\) at 5 \(m\) distance apart (where \({B}\) is vertically above \(A\,).\)
359425
A unit positive point charge of mass m is projected with a velocity \(v\) inside the tunnel which is made inside a uniformly charged non-conducting sphere of charge density \(\rho .\) The minimum velocity with which the point charge should be projected such that it can reach the opposite end of the tunnel, is equal to:
359423
An infinite plane of charge with \({\sigma=2 \epsilon_{0} \dfrac{{C}}{{m}^{2}}}\) is tilted at a \({37^{\circ}}\) angle to the vertical direction as shown below. Find the potential difference, \({V_{A}-V_{B}}\) in volts, between points \({A}\) and \({B}\) at 5 \(m\) distance apart (where \({B}\) is vertically above \(A\,).\)
359425
A unit positive point charge of mass m is projected with a velocity \(v\) inside the tunnel which is made inside a uniformly charged non-conducting sphere of charge density \(\rho .\) The minimum velocity with which the point charge should be projected such that it can reach the opposite end of the tunnel, is equal to:
359423
An infinite plane of charge with \({\sigma=2 \epsilon_{0} \dfrac{{C}}{{m}^{2}}}\) is tilted at a \({37^{\circ}}\) angle to the vertical direction as shown below. Find the potential difference, \({V_{A}-V_{B}}\) in volts, between points \({A}\) and \({B}\) at 5 \(m\) distance apart (where \({B}\) is vertically above \(A\,).\)
359425
A unit positive point charge of mass m is projected with a velocity \(v\) inside the tunnel which is made inside a uniformly charged non-conducting sphere of charge density \(\rho .\) The minimum velocity with which the point charge should be projected such that it can reach the opposite end of the tunnel, is equal to: