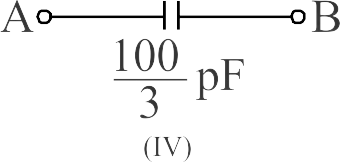359240
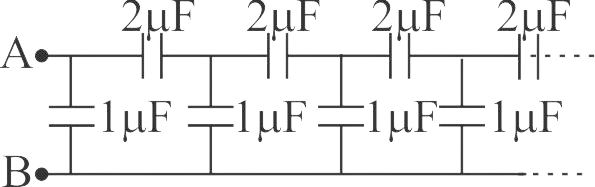
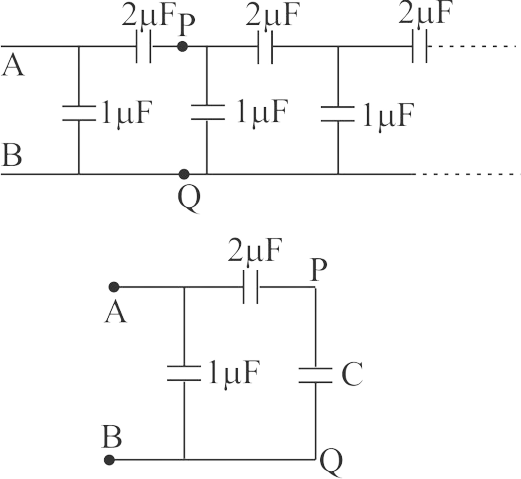
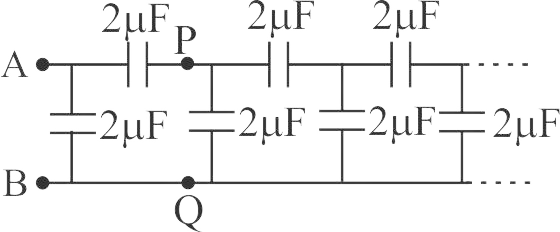
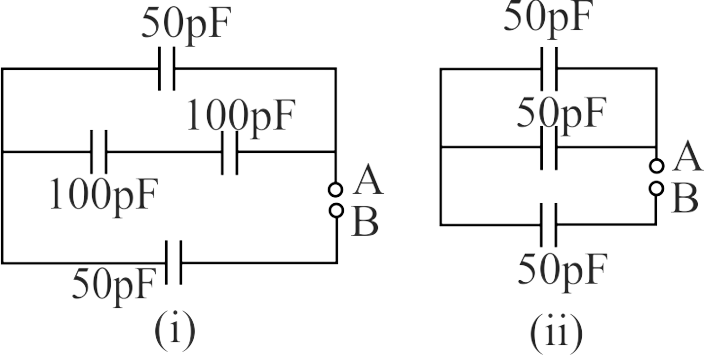
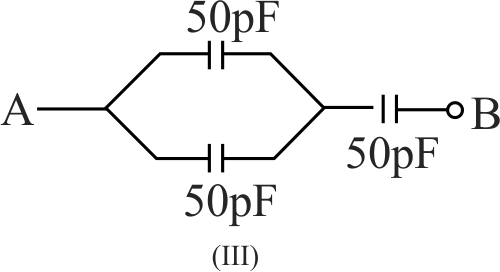
A finite ladder is constructed by connecting several sections of \(2\mu F,4\mu F\) capacitor combinations as shown in the figure. It is terminated by a capacitor of capacitance \(C\). What value should be choseen for \(C\) such that equivalent capacitance of the ladder between the points \(A\) and \(B\) becomes independent of the number of sections in between.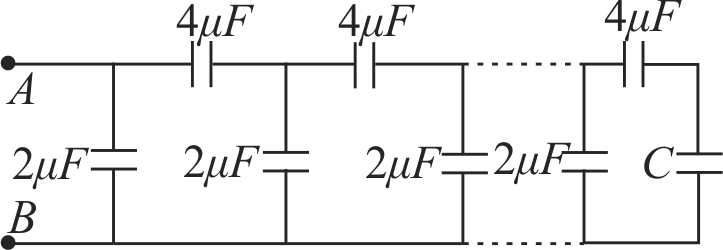
359240
A finite ladder is constructed by connecting several sections of \(2\mu F,4\mu F\) capacitor combinations as shown in the figure. It is terminated by a capacitor of capacitance \(C\). What value should be choseen for \(C\) such that equivalent capacitance of the ladder between the points \(A\) and \(B\) becomes independent of the number of sections in between.
359240
A finite ladder is constructed by connecting several sections of \(2\mu F,4\mu F\) capacitor combinations as shown in the figure. It is terminated by a capacitor of capacitance \(C\). What value should be choseen for \(C\) such that equivalent capacitance of the ladder between the points \(A\) and \(B\) becomes independent of the number of sections in between.
359240
A finite ladder is constructed by connecting several sections of \(2\mu F,4\mu F\) capacitor combinations as shown in the figure. It is terminated by a capacitor of capacitance \(C\). What value should be choseen for \(C\) such that equivalent capacitance of the ladder between the points \(A\) and \(B\) becomes independent of the number of sections in between.
359240
A finite ladder is constructed by connecting several sections of \(2\mu F,4\mu F\) capacitor combinations as shown in the figure. It is terminated by a capacitor of capacitance \(C\). What value should be choseen for \(C\) such that equivalent capacitance of the ladder between the points \(A\) and \(B\) becomes independent of the number of sections in between.